Interested Article - Плосконосая квадратная антипризма

- 2020-07-29
- 2
Плосконосая квадратная антипризма — это один из многогранников Джонсона ( J 85 , М 28 по Залгаллеру ).
Многогранник Джонсона — один из строго выпуклых многогранников , имеющих правильные грани, но не являющийся однородным (то есть он не является правильным многогранником , архимедовым телом , призмой или антипризмой ). Многогранники названы именем Нормана Джонсона , который первым перечислил эти многогранники в 1966 году .
Многогранник является одним из элементарных правильногранных многогранников, не получающихся манипуляцией «отрежь и приклей» с правильными и архимедовыми телами, и хотя тело родственно икосаэдру , оно имеет четырёхкратную симметрию, а не трёхкратную.
Тело можно получить соединением двух куполов , повёрнутых относительно друг друга.
Построение
Плосконосая квадратная антипризма строится согласно названию из квадратной антипризмы путём отсечения углов и обозначается как ss{2,8} (s{2,8} — это квадратная антипризма ).
Плосконосые антипризмы
Аналогичным образом построенный многогранник ss{2,6} — это плосконосая треугольная антипризма (треугольная антипризма — это октаэдр с неполной симметрией), то же самое, что и правильный икосаэдр . Плосконосая пятиугольная антипризма , ss{2,10}, или антипризмы с большим числом сторон могут быть построены аналогичным образом, но не как выпуклые многогранники с правильными треугольниками в качестве граней. Предшествующее тело Джонсона, плосконосый двуклиноид , конструктивно тоже попадает под эту схему как ss{2,4}, но в этом случае нужно два ребра понимать как вырожденные двуугольные грани (показаны красным цветом) дигональной антипризмы .
| Симметрия | D 2d , [2 + ,4], (2*2) | D 3d , [2 + ,6], (2*3) | D 4d , [2 + ,8], (2*4) | D 5d , [2 + ,10], (2*5) |
|---|---|---|---|---|
| Антипризмы |

s{2,4} (v:4; e:8; f:6) |

s{2,6} (v:6; e:12; f:8) |

s{2,8} (v:8; e:16; f:10) |
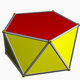
s{2,10} (v:10; e:20; f:12) |
|
Усечённые
антипризмы |
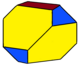
ts{2,4} (v:16;e:24;f:10) |
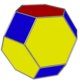
ts{2,6} (v:24; e:36; f:14) |

(v:32; e:48; f:18) |
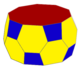
(v:40; e:60; f:22) |
| Симметрия | D 2 , [2,2] + , (222) | D 3 , [3,2] + , (322) | D 4 , [4,2] + , (422) | D 5 , [5,2] + , (522) |
|
Плосконосые
антипризмы |
J 84 (М 25 ) | Икосаэдр | J 85 (М 28 ) | Вогнутая |

ss{2,4} (v:8; e:20; f:14) |

(v:12; e:30; f:20) |

ss{2,8} (v:16; e:40; f:26) |

(v:20; e:50; f:32) |
Примечания
- , с. 169–200.
- . Дата обращения: 19 мая 2017. 27 марта 2019 года.
Литература
- Convex polyhedra with regular faces // . — 1966. — Т. 18 . — doi : .
Ссылки
- Eric W. Weisstein от 14 октября 2017 на Wayback Machine от 20 декабря 2016 на Wayback Machine на MathWorld
- 2020-07-29
- 2