Параллелоэдр ― выпуклый многогранник , параллельным перенесением которого можно замостить пространство, то есть покрыть евклидово пространство так, чтобы многогранники не входили друг в друга и не оставляли пустот между собой .

Примеры и свойства

• Параллелоэдрами являются, например, области Дирихле — Вороного решёток в евклидовом пространстве.
• На плоскости существует две разновидности параллелоэдров: параллелограммы и центрально-симметричные шестиугольники.
• В трёхмерном пространстве существует ровно пять топологических типов параллелоэдров: куб , шестиугольная призма , ромбододекаэдр , (см. рисунок) и усечённый октаэдр .

• Все параллелоэдры (любой размерности) являются центрально-симметричными многогранниками. Все гиперграни параллелоэдра также центрально-симметричны.
• В двумерном и трёхмерном случаях все параллелоэдры являются зоноэдрами . Обратно, любой зоноэдр, имеющий один из описанных топологических типов, является параллелоэдром.
• Уже в четырёхмерном пространстве не все параллелоэдры являются зоноэдрами.

История

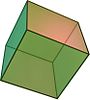
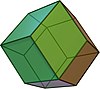
Начало теории параллелоэдров было положено в XIX веке трудами Фёдорова и Минковского .

Замечательный вклад в неё внёс Г. Ф. Вороной , доказав, что всякий примитивный параллелоэдр аффинно эквивалентен DV-области некоторой решётки.

В XX веке теорию параллелоэдров развивали Б.Н. Делоне , Б. А. Венков, С. С. Рышков , П. Макмаллен (P. Macmallen) и другие.

В последнее время изучение всех решётчатых параллелоэдров сведено к изучению так называемых коренных параллелоэдров, которые образуют в некотором роде базис параллелоэдров. Теорема о представлении любого решётчатого параллелоэдра в виде суммы Минковского конечного числа коренных параллелоэдров была сформулирована С. С. Рышковым. Подробное доказательство этой теоремы дано в совместной статье С. С. Рышкова и Е. А. Большаковой.

Примечания

Литература

• А.Д. Александров. Выпуклые многогранники. — Москва, Ленинград: Государственное издательство технико-теоретической литературы , 1950.
• / С. С. Рышков , Е. П. Барановский . - Москва : Наука, 1976. - 130 с. : ил.; 26 см. - (Труды Математического института имени В. А. Стеклова/ АН СССР; Т. 137).