Interested Article - Ротонда (геометрия)

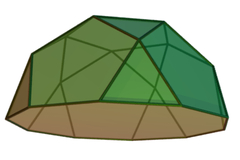
Множество ротонд
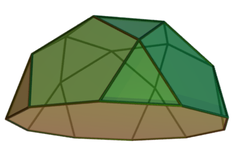
(Пример: пятискатная ротонда)
Грани	1 n-угольник 1 2n-угольник n пятиугольников 2 n треугольников
Рёбра	7 n
Вершины	4 n
Группы симметрии	, [ n ], (* nn ), порядок 2 n
	C _n , [n] ⁺ , ( nn ), порядок n
Свойства	выпуклая

Ротонда — диэдрально-симметричный многогранник . Они похожи на куполы , но вместо перемежающихся квадратов и треугольников перемежаются пятиугольники и треугольники (по отношению к оси). Пятискатная ротонда является телом Джонсона ( J ₆ ).

Другие виды ротонд можно получить с помощью диэдральной симметрии и деформированных равносторонних пятиугольников.

Биротонда

Множество биротонд
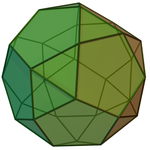
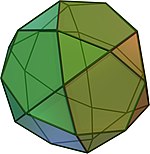
(Пример прямой и повёрнутой форм биротонд)
Грани	2 n-угольника 2 n пятиугольников 4 n треугольников
Рёбер	12 n
Вершин	6 n
Группы симметрии	Прямые: , [ n ,2], (* n 22), порядок 4 n Повёрнутые: , [ 2n ,2 ⁺ ], (2* n ), порядок 4 n
	D _n , [ n ,2] ⁺ , ( n 22), порядок 2 n
Свойства	выпуклая

Биротонда — любой член семейства диэдрально-симметричных многогранников , образованный из двух ротонд, соединённых по наибольшей грани. Эти многогранники подобны бикуполам , но вместо перемежающихся квадратов и треугольников в них перемежаются пятиугольники и треугольники (по отношению к оси). Имеется два вида биротонд — прямые и повёрнутые. Прямая биротонда состоит из ротонд, расположенных зеркально относительно друг друга, в то время как в повёрнутой биротонде одна из ротонд повёрнута относительно другой (так что пятиугольники соседствуют не с пятиугольниками, а с треугольниками).

Пятискатные биротонды можно образовать с помощью правильных граней, получая в одном случае ( J ₃₄ ), а в другом — полуправильный многогранник :

пятискатная прямая биротонда ,
пятискатная повёрнутая биротонда, которая также называется икосододекаэдром .

Другие виды биротонд можно получить с помощью диэдральной симметрии и деформированных равносторонних пятиугольников.

См. также

Примечания

Литература

. // Canadian Journal of Mathematics. — 1966. — Т. 18 . — С. 169–200 . — ISSN . — doi : . Содержит оригинальное перечисление 92 тел и гипотезу, что других нет.
Victor A. Zalgaller . Convex Polyhedra with Regular Faces. — Consultants Bureau, 1969. Первое доказательство, что существует только 92 тел Джонсона.
В. А. Залгаллер. Выпуклые многогранники с правильными гранями // Зап. научн. сем. ЛОМИ. — 1967. — Т. 2 . Доказательство, что существует только 92 тел Джонсона.