Interested Article - Дельтаэдры

Наибольший строго выпуклый дельтаэдр является правильным икосаэдром

Усечённый тетраэдр с шестиугольниками, разбитыми на треугольники. Это тело не является дельтаэдром, поскольку находящиеся в одной плоскости грани недопустимы по определению.

Дельтаэдр — это многогранник , все грани которого являются правильными треугольниками . Название взято от греческой заглавной буквы дельта ( $\Delta$ ), которая имеет форму равностороннего треугольника. Существует бесконечно много дельтаэдров, но из них только восемь выпуклы , и они имеют 4, 6, 8, 10, 12, 14, 16 и 20 граней .

Число граней, рёбер и вершин перечислены ниже для каждого из восьми дельтаэдров.

Выпуклые дельтаэдры

Всего существует 8 выпуклых дельтаэдров , 3 из которых являются платоновыми телами , а 5 — многогранниками Джонсона .

У дельтаэдра с 6 гранями некоторые вершины имеют степень 3, а некоторые — степень 4. В дельтаэдрах с 10, 12, 14 и 16 гранями некоторые вершины имеют степень 4, а некоторые — степень 5. Эти пять неправильных дельтаэдров принадлежат классу правильногранных многогранников — выпуклых многогранников с правильными многоугольниками в качестве граней.

Не существует выпуклого дельтаэдра с 18 гранями . Однако даёт пример октаэдра , который либо может быть сделан выпуклым с 18 неправильными гранями, либо с двумя наборами по три равносторонних треугольника, лежащими в одной плоскости.

Правильные дельтаэдры
Название	Изображение	Количество вершин	Количество рёбер	Количество граней	Конфигурация вершины	Группа симметрии
Правильный тетраэдр		4	6	4	4 × 3 ³	T _d , [3,3]
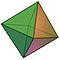
Правильный октаэдр (четырёхугольная бипирамида)		6	12	8	6 × 3 ⁴	O _h , [4,3]
Правильный икосаэдр		12	30	20	12 × 3 ⁵	I _h , [5,3]
Дельтаэдры Джонсона
Треугольная бипирамида		5	9	6	2 × 3 ³ 3 × 3 ⁴	D _3h , [3,2]
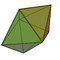
Пятиугольная бипирамида		7	15	10	5 × 3 ⁴ 2 × 3 ⁵	D _5h , [5,2]
Плосконосый двуклиноид		8	18	12	4 × 3 ⁴ 4 × 3 ⁵	D _2d , [2,2]
Трижды наращённая треугольная призма		9	21	14	3 × 3 ⁴ 6 × 3 ⁵	D _3h , [3,2]
Скрученно удлинённая четырёхугольная бипирамида		10	24	16	2 × 3 ⁴ 8 × 3 ⁵	D _4d , [4,2]

Нестрого выпуклые случаи

Существует бесконечно много дельтаэдров с копланарными (лежащими в одной плоскости) треугольниками. Если множества копланарных треугольников считаются одной гранью, можно насчитать меньше граней, рёбер и вершин. Копланарные треугольные грани могут быть слиты в ромбические, трапециевидные, шестиугольные или другие равносторонние многоугольные грани. Каждая грань должна быть выпуклым полиамондом , таким как , , , , , , и , ...

Некоторые небольшие примеры

Копланарные дельтаэдры
Название	Граней	Рёбер	Вершин	Конфигурации вершин	Группа симметрии
Наращение 1 тетр. + 1 окт.	10	15	7	1 × 3 ³ 3 × 3 ⁴ 3 × 3 ⁵ 0 × 3 ⁶	C _3v , [3]
Наращение 1 тетр. + 1 окт.	4 3	12	7	1 × 3 ³ 3 × 3 ⁴ 3 × 3 ⁵ 0 × 3 ⁶	C _3v , [3]
Наращение 2 тетр. + 1 окт.	12	18	8	2 × 3 ³ 0 × 3 ⁴ 6 × 3 ⁵ 0 × 3 ⁶	C _3v , [3]
Наращение 2 тетр. + 1 окт.	6	12	8	2 × 3 ³ 0 × 3 ⁴ 6 × 3 ⁵ 0 × 3 ⁶	C _3v , [3]
Наращение 2 тетр. + 1 окт.	12	18	8	2 × 3 ³ 1 × 3 ⁴ 4 × 3 ⁵ 1 × 3 ⁶	C _2v , [2]
Наращение 2 тетр. + 1 окт.	2 2 2	11	7	2 × 3 ³ 1 × 3 ⁴ 4 × 3 ⁵ 1 × 3 ⁶	C _2v , [2]
Треугольная усечённая пирамида Наращение 3 тетр. + 1 окт.	14	21	9	3 × 3 ³ 0 × 3 ⁴ 3 × 3 ⁵ 3 × 3 ⁶	C _3v , [3]
Треугольная усечённая пирамида Наращение 3 тетр. + 1 окт.	1 3 1	9	6	3 × 3 ³ 0 × 3 ⁴ 3 × 3 ⁵ 3 × 3 ⁶	C _3v , [3]
Наращение 2 тетр. + 2 окт.	16	24	10	0 × 3 ³ 4 × 3 ⁴ 4 × 3 ⁵ 2 × 3 ⁶	D _2h , [2,2]
Наращение 2 тетр. + 2 окт.	4 4	12	6	0 × 3 ³ 4 × 3 ⁴ 4 × 3 ⁵ 2 × 3 ⁶	D _2h , [2,2]
Тетраэдр Наращение 4 тетр. + 1 окт.	16	24	10	4 × 3 ³ 0 × 3 ⁴ 0 × 3 ⁵ 6 × 3 ⁶	T _d , [3,3]
Тетраэдр Наращение 4 тетр. + 1 окт.	4	6	4	4 × 3 ³ 0 × 3 ⁴ 0 × 3 ⁵ 6 × 3 ⁶	T _d , [3,3]
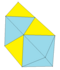
Наращение 3 тетр. + 2 окт.	18	27	11	1 × 3 ³ 2 × 3 ⁴ 5 × 3 ⁵ 3 × 3 ⁶	D _2h , [2,2]
Наращение 3 тетр. + 2 окт.	2 1 2 2	14	9	1 × 3 ³ 2 × 3 ⁴ 5 × 3 ⁵ 3 × 3 ⁶	D _2h , [2,2]
	18	27	11	0 × 3 ³ 2 × 3 ⁴ 8 × 3 ⁵ 1 × 3 ⁶	C _2v , [2]
	12 2	22	10	0 × 3 ³ 2 × 3 ⁴ 8 × 3 ⁵ 1 × 3 ⁶	C _2v , [2]
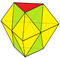
Наращение 6 тетр. + 2 окт.	20	30	12	0 × 3 ³ 3 × 3 ⁴ 6 × 3 ⁵ 3 × 3 ⁶	D _3h , [3,2]
Наращение 6 тетр. + 2 окт.	2 6	15	9	0 × 3 ³ 3 × 3 ⁴ 6 × 3 ⁵ 3 × 3 ⁶	D _3h , [3,2]
Трёхскатный купол Наращение 4 тетр. + 3 окт.	22	33	13	0 × 3 ³ 3 × 3 ⁴ 6 × 3 ⁵ 4 × 3 ⁶	C _3v , [3]
Трёхскатный купол Наращение 4 тетр. + 3 окт.	3 3 1 1	15	9	0 × 3 ³ 3 × 3 ⁴ 6 × 3 ⁵ 4 × 3 ⁶	C _3v , [3]
Треугольная бипирамида Наращение 8 тетр. + 2 окт.	24	36	14	2 × 3 ³ 3 × 3 ⁴ 0 × 3 ⁵ 9 × 3 ⁶	D _3h , [3]
Треугольная бипирамида Наращение 8 тетр. + 2 окт.	6	9	5	2 × 3 ³ 3 × 3 ⁴ 0 × 3 ⁵ 9 × 3 ⁶	D _3h , [3]
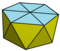
Шестиугольная антипризма	24	36	14	0 × 3 ³ 0 × 3 ⁴ 12 × 3 ⁵ 2 × 3 ⁶	D _6d , [12,2 ⁺ ]
Шестиугольная антипризма	12 2	24	12	0 × 3 ³ 0 × 3 ⁴ 12 × 3 ⁵ 2 × 3 ⁶	D _6d , [12,2 ⁺ ]
Усечённый тетраэдр Наращение 6 тетр. + 4 окт.	28	42	16	0 × 3 ³ 0 × 3 ⁴ 12 × 3 ⁵ 4 × 3 ⁶	T _d , [3,3]
Усечённый тетраэдр Наращение 6 тетр. + 4 окт.	4 4	18	12	0 × 3 ³ 0 × 3 ⁴ 12 × 3 ⁵ 4 × 3 ⁶	T _d , [3,3]
Октаэдр Наращение 8 тетр. + 6 окт.	32	24	18	0 × 3 ³ 12 × 3 ⁴ 0 × 3 ⁵ 6 × 3 ⁶	O _h , [4,3]
Октаэдр Наращение 8 тетр. + 6 окт.	8	12	6	0 × 3 ³ 12 × 3 ⁴ 0 × 3 ⁵ 6 × 3 ⁶	O _h , [4,3]

Невыпуклые дельтаэдры

Невыпуклых и тороидальных дельтаэдров существует бесконечно много.

Пример дельтаэдра с самопересекающимися гранями

Большой икосаэдр — тело Кеплера — Пуансо , с 20 пересекающимися треугольниками

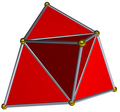
Другие невыпуклые дельтаэдры можно получить путём добавления пирамид к граням всех 5 правильных многогранников:

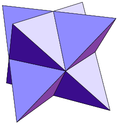
Триакистетраэдр	Тетракисгексаэдр	Триакисоктаэдр ( stella octangula )	Пентакисдодекаэдр	Триакисикосаэдр

12 треугольников	24 треугольников		60 треугольников

Другие наращения тетраэдров:

Примеры: Наращенные тетраэдры
8 треугольников	10 треугольников	12 треугольников

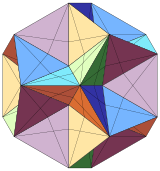
Также путём добавления к граням перевёрнутых пирамид:

60 треугольников	48 треугольников
	Тороидальный дельтаэдр

Примечания

, с. 115–128.
. Дата обращения: 6 июня 2016. 26 сентября 2020 года.
, с. 55–57.
. Дата обращения: 13 октября 2017. 19 октября 2015 года.

Литература

Freudenthal H. , van der Waerden B. L. Over een bewering van Euclides ("On an Assertion of Euclid") // . — 1947. — Т. 25 . — С. 115–128 . (Авторы показали, что существует только 8 выпуклых дельтаэдров. )
Charles W. Trigg. // Mathematics Magazine. — 1978. — Т. 51 , вып. 1 . — С. 55–57 . — JSTOR .