Додекаэдр Билинского — многогранник ( зоноэдр ), составленный из 12 одинаковых золотых ромбов .

Топологически изоморфен ромбододекаэдру , но, в отличие от него, не является изоэдральным (хотя всего его грани также конгруэнтны ) и имеет другую группу симметрии .

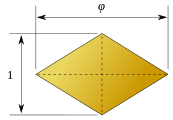
Грани додекаэдра Билинского — ромбы с отношением диагоналей, равным золотому сечению ${\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618;}$ они несколько более вытянуты, чем грани ромбододекаэдра, представляющие собой ромбы с отношением диагоналей ${\displaystyle {\sqrt {2}}\approx 1{,}414.}$

• 
  Грань ромбододекаэдра
• 
  Грань додекаэдра Билинского

Имеет 14 вершин. В 2 вершинах сходятся четыре грани своими острыми углами; в 4 вершинах сходятся три грани тупыми углами; в 4 вершинах сходятся одна грань острым углом и две тупыми; в 4 вершинах сходятся три грани острыми углами и одна тупым.

У додекаэдра Билинского 24 ребра равной длины. При 12 рёбрах (примыкающих к вершинам, отмеченным на рисунке красным ) двугранные углы равны ${\displaystyle 144^{\circ };}$ при 8 рёбрах (между зелёной и синей вершинами) — ${\displaystyle 108^{\circ };}$ при 4 рёбрах (между чёрной и зелёной вершинами) — ${\displaystyle 72^{\circ }.}$

В координатах

Додекаэдр Билинского можно расположить в декартовой системе координат так, чтобы его вершины имели координаты

• ${\displaystyle \left(0;\;0;\;\pm \Phi ^{2}\right),}$
• ${\displaystyle \left(0;\;\pm 1;\;\pm 1\right),}$
• ${\displaystyle \left(\pm \Phi ;\;0;\;\pm \Phi \right),}$
• ${\displaystyle \left(\pm \Phi ;\;\pm 1;\;0\right).}$

При этом центр симметрии многогранника будет совпадать с началом координат, три оси симметрии — с осями Ox, Oy и Oz, а три плоскости симметрии — с плоскостями xOy, xOz и yOz.

Метрические характеристики

Если додекаэдр Билинского имеет ребро длины ${\displaystyle a}$ , его площадь поверхности и объём выражаются как

${\displaystyle S={\frac {24}{\sqrt {5}}}\;a^{2}\approx 10{,}7331263a^{2},}$

${\displaystyle V={\frac {4}{5}}{\sqrt {5+2{\sqrt {5}}}}\;a^{3}\approx 2{,}4621468a^{3}.}$

История

Впервые данный многогранник встречается под названием «додекаромб» в 1752 году на иллюстрации в книге английского математика .

Заново найден в 1960 году хорватским математиком Станко Билинским , который назвал его «ромбическим додекаэдром второго рода» . Открытие Билинского заполнило остававшийся незамеченным 75 лет пробел в классификации выпуклых многогранников с конгруэнтными ромбическими гранями, описанной Евграфом Фёдоровым .

Гарольд Коксетер в статье 1962 года ошибочно утверждал, что додекаэдр Билинского может быть получен аффинным преобразованием ромбододекаэдра. Это утверждение ложно .

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
• David I. McCooey.