Interested Article - Теорема Коши о многогранниках

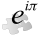
Теорема Коши о многогранниках утверждает, что грани многогранника вместе с правилом склейки полностью определяют выпуклый многогранник.

Формулировка

Два замкнутых выпуклых многогранника конгруэнтны , если существует непрерывная биекция между их поверностями перводящая изометрией каждую грань первого многогранника в грань второго.

История

Вопрос о том, что грани многогранника вместе с правилами склейки полностью определяют выпуклый многогранник был сформулирован Лежандром в 1-м издании его учебника. Там же была дана ключевая лемма о четырёх переменах знаков, которая использовалась Коши в его доказательстве. Это доказательство содержало ошибку, которая была замечена Штейницем и исправлена только в 1934 году .

Вариации и обобщения

Аналогичный результат верен в пространствах всех размерностей начиная с 3.

Для невыпуклых многогранников аналогичный результат неверен.
- Более того, существует невыпуклый многогранник, который допускает непрерывные деформации в классе многогранников с конгруэнтными гранями. Такой многогранник называется изгибаемым . Однако, согласно теореме Сабитова, объём такого многогранника в процессе деформаций будет оставаться неизменным.

Согласно теореме Александрова о развёртке , условие конгруэнтности граней можно ослабить до условия изометричности внутренней метрики поверхности многогранника.
- Более того, то же верно для любой замкнутой выпуклой поверхности (теорема Погорелова ).

См. также

Лемма о руке

Примечания

Legendre, A. M. "Éléments de géométrie". Paris, 1794. Note XII. P. 321–334.
Cauchy A. L. Sur les polygones et polyèdres, Second mémoire // J. de l’École Polytechnique. 1813. V. 9. P. 87–98.
Steinitz E., Rademacher H. Vorlesungen ̈uber die Theorie der Polyeder. Berlin: Springer-Verl., 1934.

Литература

Н. П. Долбилин, . М.: МЦНМО, 2000. 40 с. ISBN 5-900916-48-0 ; Тираж 2000 экз. Серия Библиотека «Математическое просвещение», выпуск 5.
Лекция 24 в Табачников С. Л., Фукс Д. Б. . — МЦНМО, 2011. — 512 с. — 2000 экз. — ISBN 978-5-94057-731-7 .