Interested Article - Многогранник Часара

- 2020-04-27
- 1
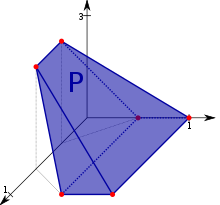
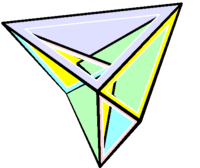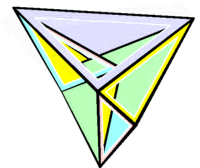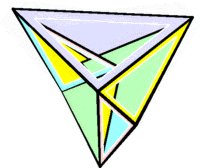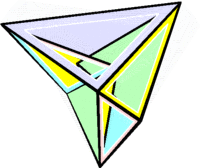
Многогранник Часара — невыпуклый многогранник , топологически эквивалентный тору , с 14 треугольными гранями.
Этот многогранник не имеет диагоналей — любая пара вершин связана ребром. Семь вершин и 21 ребро многогранника Часара образуют вложение полного графа в топологический тор . Из 35 возможных треугольников, образованных вершинами многогранника, только 14 являются гранями. Если семь вершин пронумеровать числами от 1 до 7, тор можно разрезать на лист, топологически эквивалентный следующему:
5———4———7———2
/ \ / \ / \ / \
6———1———3———5———4
/ \ / \ / \ /
4———7———2———6
\ /
4
Этот шаблон можно использовать для замощения плоскости. На рисунке сверху грани следующие (вершина 1 наверху фигуры):
- Голубые:
(1, 2, 3) (1, 3, 4) (1, 4, 5) (1, 5, 6) (1, 6, 7) (1, 7, 2)
- Красные
(2, 3, 6) (6, 3, 5)
- Жёлтые
(3, 5, 7) (7, 5, 2)
- Зелёные
(6, 2, 4) (4, 2, 5)
- Синие
(4, 6, 7) (4, 7, 3)
При такой нумерации расположение вершин в конце видеоклипа (по часовой стрелке, начиная с 1) следующее: 1, 2, 5, 4, 3, 7, 6, 5, 2, 7, 3, 4, 5, 6, 7.
Есть некоторая свобода в расстановке вершин, но некоторые расстановки ведут к пересечению граней и отверстие не образуется.
Все вершины топологически эквивалентны, как можно видеть из замощения плоскости на иллюстрации выше.
Тетраэдр и многогранник Часара являются двумя единственными многогранниками (имеющие границей многообразие ) без диагоналей, хотя имеются другие многогранники, такие как многогранник Шёнхардта , которые не имеют внутренних диагоналей (то есть все диагонали многогранника находятся вне многогранника), а также поверхности без диагоналей, не являющиеся многообразиями . Если многогранник с v вершинами вложен в поверхность с h дырами таким образом, что любая пара вершин соединена ребром, из эйлеровой характеристики следует, что
Это равенство выполняется для тетраэдра с h = 0 и v = 4 и для многогранника Часара с h = 1 и v = 7. Следующее возможное решение — h = 6 и v = 12 — могло бы соответствовать многограннику с 44 гранями и 66 рёбрами, но его нельзя реализовать. Неизвестно, существуют ли многогранники с бо́льшим родом . В общем случае это равенство может быть удовлетворено только при v , равном 0, 3, 4 или 7 по модулю 12 .
Многогранник Часара назван именем венгерского тополога , обнаружившего многогранник в 1949 году. Двойственный многограннику Часара многогранник Силаши был найден в 1977 . У него 14 вершин, 21 ребро и семь шестиугольных граней, при этом каждые две грани имеют общее ребро. Подобно многограннику Часара, многогранник Силаши имеет топологию тора.
Примечания
- .
- .
- .
- .
Литература
- A. Császár. A polyhedron without diagonals // Acta Sci. Math. Szeged. — 1949. — Т. 13 . — P. 140–142.
-
Martin Gardner.
. — W. H. Freeman and Company, 1988. — С.
–152. —
ISBN 0-7167-1924-X
.
- Мартин Гарднер. Глава 11 «Полиэдр Часара» // Путешествие во времени. — Москва: «Мир», 1990. — С. 165—178. — ISBN 5-03-001166-8 .
- Martin Gardner. . — W. H. Freeman and Company, 1992. — С. –120. — ISBN 0-7167-2188-0 .
- Frank H. Lutz. // Electronic Geometry Models. — 2001.
- Sándor Szabó. Polyhedra without diagonals // Periodica Mathematica Hungarica. — 1984. — Т. 15 , вып. 1 . — С. 41—49 . — doi : .
- Sándor Szabó. Polyhedra without diagonals II // Periodica Mathematica Hungarica. — 2009. — Т. 58 , вып. 2 . — С. 181—187 . — doi : .
- Günter M. Ziegler. Discrete Differential Geometry / A. I. Bobenko, P. Schröder, J. M. Sullivan, G. M. Ziegler. — Springer-Verlag, 2008. — Т. 38. — С. 191—213. — (Oberwolfach Seminars). — ISBN 978-3-7643-8620-7 . — doi : .
Ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- 2020-04-27
- 1