Перестановочный многогранник (или пермутоэдр ) порядка ${\displaystyle n}$ — это ( ${\displaystyle n-1}$ )-мерный выпуклый многогранник , вложенный в ${\displaystyle n}$ -мерное евклидово пространство, который является выпуклой оболочкой ${\displaystyle n!}$ точек, получающихся перестановками координат вектора ${\displaystyle (1,2,3,\ldots ,n)}$ .

История

Согласно , перестановочный многогранник впервые появляется в работах в 1911 году. Сам термин «перестановочный многогранник» (точнее, его французский вариант «permutoèdre») впервые появился в статье Гуибуда (G.-T.Guibaud) и в 1963 году. Предлагая его, авторы писали, что «permutoèdre» выглядит варварски, но легко запоминается и что они оставляют использование этого термина на усмотрение читателя.

Близким понятием является многогранник Биркгофа , определяемый как выпуклая оболочка матриц перестановок . В более общей ситуации Боуман (V.-J.Bowman) в 1972 году использовал термин «перестановочный многогранник» («permutation polytope») для любого многогранника, вершины которого находятся во взаимно однозначном соответствии с перестановками некоторого множества.

Свойства

• Перестановочный многогранник порядка n имеет n ! вершин, каждая из которых соединена с n − 1 другими вершинами, так что общее число рёбер равно ( n − 1) n !/2.
• Каждое ребро имеет длину √2 и соединяет две вершины, получающиеся друг из друга перестановкой двух координат при условии, что значения этих координат различаются на единицу.

• Перестановочный многогранник имеет одну для каждого непустого собственного подмножества S множества {1, 2, 3, …, n }, состоящую из всех вершин, у которых все координаты с номерами, вошедшими в S , имеют меньшие значения, чем все координаты с номерами, не вошедшими в S . Отсюда следует, что общее число гиперграней равно 2 ⁿ − 2.

• Перестановочный многогранник является вершинно-транзитивным, а именно: симметрическая группа S _n действует на множестве вершин перестановочного многогранника посредством перестановок координат.

• Перестановочный многогранник является зонотопом ; параллельная копия перестановочного многогранника может быть получена как сумма Минковского n ( n − 1)/2 прямолинейных отрезков, соединяющих все пары векторов .

• Неориентированный граф , образованный вершинами и рёбрами перестановочного многогранника, изоморфен графу Кэли симметрической группы.

Замощение пространства

Перестановочный многогранник порядка n полностью содержится в ( n − 1)-мерной гиперплоскости, состоящей из всех точек, сумма координат которых равна

1 + 2 + … + n = n ( n + 1)/2.

Более того, эта гиперплоскость может быть (англ.) бесконечным количеством параллельных копий перестановочного многогранника. Каждая из этих копий отличается от исходного перестановочного многогранника на элемент некоторой ( n − 1)-мерной решётки , образованной n -мерными векторами, все координаты которых целочисленные, их сумма равна нулю, причём все координаты принадлежат одному классу вычетов по модулю n :

x ₁ + x ₂ + … + x _n = 0, x ₁ ≡ x ₂ ≡ … ≡ x _n (mod n ).

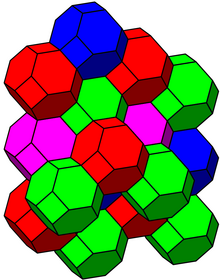
Например, перестановочный многогранник порядка 4, изображённый на рисунке, замощает 3-мерное пространство посредством параллельных переносов. Здесь 3-мерное пространство рассматривается как аффинное подпространство 4-мерноего пространства R ⁴ с координатами x , y , z , w , которое образовано четвёрками вещественных чисел, сумма которых равна 10, то есть

x + y + z + w = 10.

Легко проверить, что для каждого из следующих четырёх векторов

(1,1,1,−3), (1,1,−3,1), (1,−3,1,1) и (−3,1,1,1),

сумма координат равна нулю и все координаты сравнимы с 1 по модулю 4. Любые три из этих векторов порождают решётку параллельных переносов.

Замощения, построенные таким способом из перестановочных многогранников порядка 3 и 4, являются замощением правильными шестиугольниками и (англ.) соответственно.

Галерея

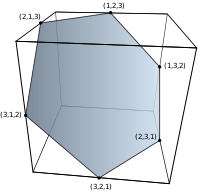
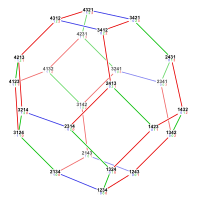
Порядок 2	Порядок 3	Порядок 4
2 вершины	6 вершин	24 вершины
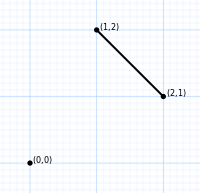
Перестановочный многогранник порядка 2 — это отрезок на диагонали единичного квадрата .	Перестановочный многогранник порядка 3 — это правильный шестиугольник , являющийся сечением 2×2×2 куба .	Перестановочный многогранник порядка 4 — это .

Порядок 5	Порядок 6
120 вершин	720 вершин
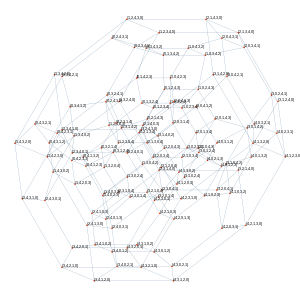
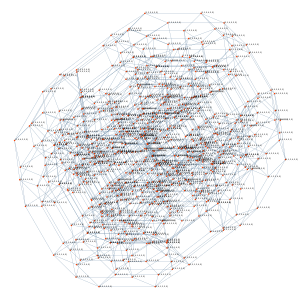
Перестановочный многогранник порядка 5.	Перестановочный многогранник порядка 6.

Замечания

Литература

• Bowman, V. J. (1972), , SIAM Journal on Applied Mathematics , 22 (4): 580—589, doi : .
• Gaiha, P.; Gupta, S. K. (1977), , SIAM Journal on Applied Mathematics , 32 (2): 323—327, doi : .
• Guilbaud, Georges-Théodule; [in английский] (1963), , Mathématiques et sciences humaines , 4 : 9—33 от 5 июня 2011 на Wayback Machine .
• Le Conte de Poly-Barbut, Cl. (1990), "Le diagramme du treillis permutoèdre est intersection des diagrammes de deux produits directs d'ordres totaux", Mathématiques, Informatique et Sciences Humaines , 112 : 49—53 .
• Santmyer, Joe (2007), , Mathematics Magazine , 80 (2): 120—125
• [in английский] (1911), "Analytic treatment of the polytopes regularly derived from the regular polytopes", Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam , 11 (3): 87 pp.
• [in английский] (1995), Lectures on Polytopes , Springer-Verlag, Graduate Texts in Mathematics 152
• Гарбер, А.И.; Поярков, А.П. (2006), "О перестановочных многогранниках", Вестник МГУ, серия 1 (2): 3—8 .

Ссылки

• Bryan Jacobs. (англ.) на сайте Wolfram MathWorld .
• Alexander Postnikov (2005). "Permutohedra, associahedra, and beyond". arXiv : . {{ cite arXiv }} : |class= игнорируется ( справка )