Тензорной алгеброй линейного пространства ${\displaystyle V}$ (обозначается ${\displaystyle T(V)}$ ) называется алгебра тензоров любого ранга над ${\displaystyle V}$ с операцией тензорного умножения.

Также тензорной алгеброй называется соответствующий раздел линейной алгебры (то есть раздел, занимающийся тензорами , определёнными над одним линейным пространством, в отличие от тензорного анализа , занимающегося тензорными полями, заданными на касательном расслоении многообразия и дифференциальными соотношениями для этих полей).

Определение

Пусть V — векторное пространство над полем K . Для любого натурального числа k определим k -ую тензорную степень V как тензорное произведение V на себя k раз:

${\displaystyle T^{k}V=V^{\otimes k}=V\otimes V\otimes \cdots \otimes V}$

Таким образом, T ^k V состоит из всех тензоров над V ранга k . Будем считать, что T ⁰ V — это основное поле K (одномерное векторное пространство над собой).

Определим T ( V ) как прямую сумму T ^k V для всех k = 0,1,2,…

${\displaystyle T(V)=\bigoplus _{k=0}^{\infty }T^{k}V=K\oplus V\oplus (V\otimes V)\oplus (V\otimes V\otimes V)\oplus \cdots }$

Умножение в T ( V ) определяется задаваемым тензорным произведением каноническим изоморфизмом :

${\displaystyle T^{k}V\otimes T^{\ell }V\to T^{k+\ell }V}$

который потом продолжается по линейности на всю T ( V ). Такое умножение превращает тензорную алгебру T ( V ) в градуированную алгебру .

Универсальное свойство и функториальность

Тензорная алгебра T ( V ) — это свободная алгебра векторного пространства V . Как и для любой другой , функтор Т является левым сопряженным функтором забывающего функтора (который в данном случае отправляет К-алгебру в её векторное пространство). Тензорная алгебра удовлетворяет следующему универсальному свойству , которое формализует утверждение, что это наиболее общая алгебра, содержащая пространство V :

Любое линейное отображение ${\displaystyle f:V\to A}$ пространства V над полем К в алгебру A над K может быть единственным образом продолжено до гомоморфизма алгебр ${\displaystyle {\bar {f}}:T(V)\to A}$ . Это утверждение выражается коммутативной диаграммой :

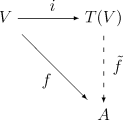
где i — каноническое вложение V в T ( V ). Тензорную алгебру можно определить как единственную (с точностью до изоморфизма ) алгебру, обладающую таким свойством, хотя необходимо ещё явно показать, что такая алгебра существует.

Приведенное выше универсальное свойство показывает, что тензорная алгебра функториальна , то есть T — это функтор из категории K -Vect векторных пространств над K в категорию K -Alg K -алгебр. Функториальность Т означает, что любое линейное отображение из V в W может быть единственным образом продолжено до гомоморфизма из алгебры T(V) в T(W).

Некоммутативные многочлены

Если размерность V конечна и равна n , то тензорную алгебру можно рассматривать как алгебру многочленов над K с n некоммутативными переменными. Базисным векторам V соответствуют некоммутативные переменные, причем их умножение будет ассоциативным, дистрибутивным и K -линейным.

Заметим, что алгебра многочленов над V — это не ${\displaystyle T(V)}$ , а ${\displaystyle T(V^{*})}$ : однородная линейная функция на V является элементом сопряженного пространства ${\displaystyle V^{*}}$ .

Факторалгебры

В силу общности тензорной алгебры многие другие важные алгебры пространства V можно получить, накладывая определенные ограничения на образующие элементы тензорной алгебры, то есть строя факторалгебры от T ( V ). Например, так можно построить внешнюю алгебру , симметрическую алгебру и алгебру Клиффорда .

Вариации и обобщения

Конструкция тензорной алгебры над линейным пространством естественно обобщается до тензорной алгебры над модулем M над коммутативным кольцом . Если R — некоммутативное кольцо , можно построить тензорное произведение для любых R - бимодулей над M . Для обычных R -модулей оказывается невозможным построить кратное тензорное произведение.

Ссылки

• Винберг Э. Б. Курс алгебры — М. :Издательство «Факториал Пресс» — 2002, ISBN 5-88688-060-7

См. также

• Алгебра Клиффорда
• Внешняя алгебра
• Симметрическая алгебра