Interested Article - Эллипсоид вращения

- 2021-06-20
- 1



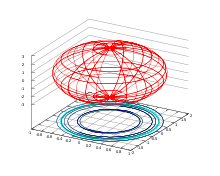
Эллипсо́ид враще́ния (сферо́ид) — поверхность вращения в трёхмерном пространстве , образованная при вращении эллипса вокруг одной из его .
Термин «сфероид» для обозначения двух вариантов эллипсоида вращения ввёл Архимед : «… мы полагаем следующее: если эллипс при сохранении неподвижной большей оси поворачивается, возвращаясь в исходное положение, то охватываемая им фигура будет называться вытянутым сфероидом (παραμακες σφαιροιδες). Если эллипс поворачивается при сохранении в неподвижности малой оси и возвращается назад, то охватываемая им фигура будет называться сплюснутым сфероидом (επιπλατυ σφαιροιδες).»
Эллипсоид вращения является частным случаем эллипсоида , две из трёх полуосей которого имеют одинаковую длину
( ):
В частном случае, когда все три полуоси равны, исходный эллипс представляет собой окружность , а эллипсоид вращения вырождается в сферу .
Вытянутый эллипсоид вращения
Вытянутый эллипсоид вращения (вытянутый сфероид) можно также определить как геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек ( фокусов ) постоянна.
Зеркало в виде вытянутого эллипсоида вращения обладает следующим свойством: лучи света, исходящие из одного из фокусов эллипсоида, после отражения соберутся в другом фокусе.
Сплюснутый эллипсоид вращения
Сплюснутый эллипсоид вращения (сплюснутый сфероид) можно также определить как геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна.
Основные формулы
- Площадь поверхности:
-
- сплюснутый эллипсоид вращения ( ):
- где
- вытянутый эллипсоид вращения ( ):
- где
- Объём:
Примеры
Форма Земли — с хорошим приближением представляет собой сплюснутый эллипсоид вращения с .
Применение
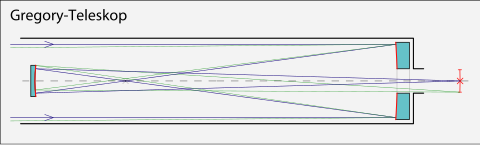
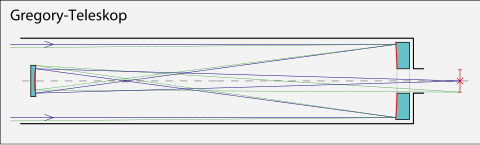
Свойство вытянутого эллипсоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Грегори и в .

|
|
|||||||||
|
Слева — радиотелескоп
РТ-70
, исполненный по системе антенны Грегори.
Справа — оптическая схема телескопа Грегори; малое зеркало имеет форму вытянутого эллипсоида вращения |
||||||||||
Примечания
- L. Russo. (неопр.) . — Springer, Berlin, 2004. — С. .
- 2021-06-20
- 1