Алгебраическая группа
- 1 year ago
- 0
- 0
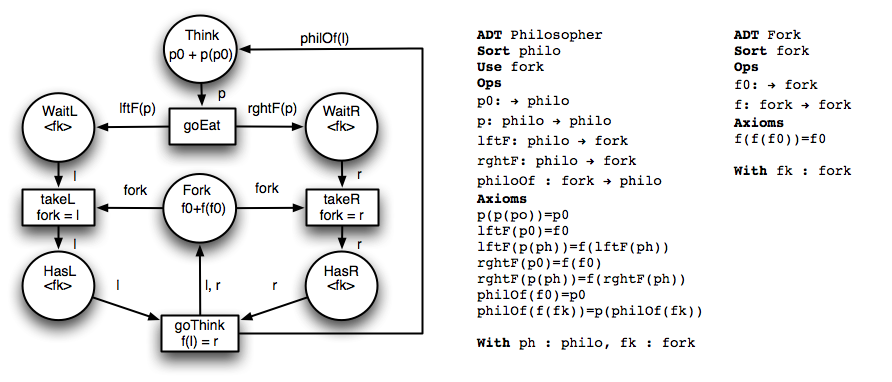
Алгебраическая сеть Петри ( англ. algebraic Petri net, APN ) — расширение обычных сетей Петри , в котором обычные маркеры заменены на элементы алгебраических типов данных . Этот формализм во многом подобен раскрашенным сетям Петри , однако в случае алгебраических сетей семантика типов данных задаётся системой аксиом , позволяющей осуществлять с её использованием доказательства и вычисления над типами.
Впервые введены Жаком Вотереном в 1985 году , усовершенствованы Вольфгангом Райзигом .
Формализм включает две составляющие:
Сами алгебраические типы данных могут быть разделены на две части:
Управляющая часть включает:
В момент активации события произведённые маркеры перемещаются в целевые позиции выходных дуг. Для того, чтобы определить семантику операций, проверить выполняются ли заданные условия и вычислить выходные термы, как правило используют техники переписывания термов .
Алгебраические сети Петри послужили базой для развития более сложных вариантов того же формализма, в частности ( Concurrent Object-Oriented Petri Nets ).
Пример алгебраической сети Петри, предназначенной для моделирования задачи об обедающих философах :
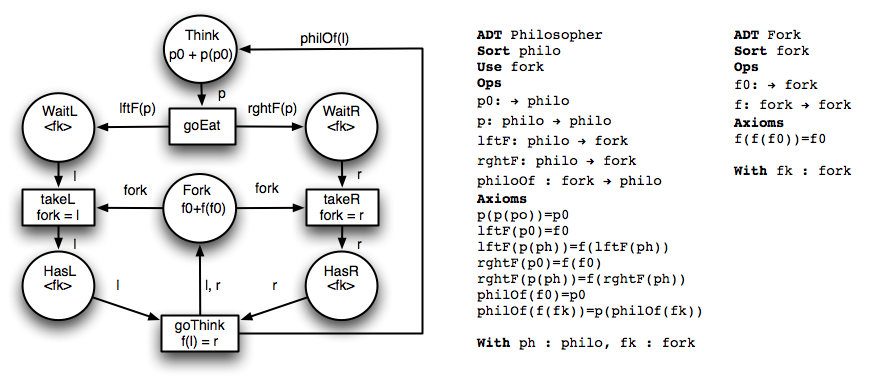
Используются два алгебраических типа данных. Один из них (
Fork
) задаёт алгебру вилок, другой (
Philosopher
) — алгебру философов. Поскольку все философы могут взять левую вилку, не взяв правую, выполнение этой модели может привести ко
взаимной блокировке
. На старте работы модели возможен только переход
goEat
. Если хотя бы один
goEat
был активирован, разрешёнными становятся также переходы
takeL
и
takeR
.