Interested Article - Почти многогранник Джонсона

- 2020-09-11
- 1
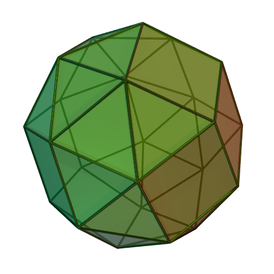
Почти многогранник Джонсона — строго выпуклый многогранник , в котором грани близки к правильным многоугольникам , но некоторые или все из них не совсем правильные. Понятие обобщает многогранники Джонсона и «часто могут физически построены без заметного отличия» неправильных граней от правильных. Точное число «почти» многогранников Джонсона зависит от требований, насколько точно грани приближаются к правильным многоугольникам.
Примеры
|
Название
Название по Конвею |
Рисунок |
Вершинная
конфигурация |
V | E | F | F 3 | F 4 | F 5 | F 6 | F 8 | F 10 | F 12 | Симметрия |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
t6kT |

|
4 (5.5.5)
24 (5.5.6) |
28 | 42 | 16 | 12 | 4 |
T
d
, [3,3]
порядок 24 |
|||||
|
cC |

|
24 (4.6.6)
8 (6.6.6) |
32 | 48 | 18 | 6 | 12 |
O
h
, [4,3]
порядок 48 |
|||||
| -- |

|
12 (5.5.6)
6 (3.5.3.5) 12 (3.3.5.5) |
30 | 54 | 26 | 12 | 12 | 2 |
D
6h
, [6,2]
порядок 24 |
||||
| -- |

|
6 (5.5.5)
9 (3.5.3.5) 12 (3.3.5.5) |
27 | 51 | 26 | 14 | 12 |
D
3h
, [3,2]
порядок 12 |
|||||

|
4 (5.5.5)
12 (3.5.3.5) 12 (3.3.5.5) |
28 | 54 | 28 | 16 | 12 |
T
d
, [3,3]
порядок 24 |
||||||
|
cD |

|
60 (5.6.6)
20 (6.6.6) |
80 | 120 | 42 | 12 | 30 |
I
h
, [5,3]
порядок 120 |
|||||
|
rtI |

|
60 (3.5.3.6)
30 (3.6.3.6) |
90 | 180 | 92 | 60 | 12 | 20 |
I
h
, [5,3]
порядок 120 |
||||
|
Усечённый усечённый икосаэдр
ttI |

|
120 (3.10.12)
60 (3.12.12) |
180 | 270 | 92 | 60 | 12 | 20 |
I
h
, [5,3]
порядок 120 |
||||
|
Расширенный усечённый икосаэдр
etI |

|
60 (3.4.5.4)
120 (3.4.6.4) |
180 | 360 | 182 | 60 | 90 | 12 | 20 |
I
h
, [5,3]
порядок 120 |
|||
|
Плосконосый полностью усечённый усечённый икосаэдр
stI |

|
60 (3.3.3.3.5)
120 (3.3.3.3.6) |
180 | 450 | 272 | 240 | 12 | 20 |
I
, [5,3]
+
порядок 60 |
Почти многогранники Джонсона с копланарными гранями
Некоторые кандидаты в почти многогранники Джонсона имеют копланарные грани. Эти многогранники можно чуть деформировать так, что грани будут сколь угодно близки к правильным многоугольникам. Эти случаи используют вершинные фигуры 4.4.4.4 квадратной мозаики , вершинные фигуры 3.3.3.3.3.3 треугольной мозаики , а также ромбы с углом 60º, делённые на два правильных треугольника, или трапеции с углом 60º как три правильных треугольника.
Примеры: 3.3.3.3.3.3
-
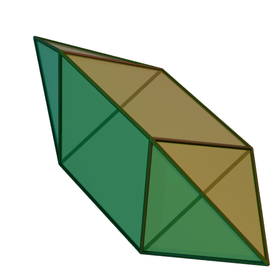
 Ромбическая призма
Ромбическая призма -

-
![Треугольный трапецоэдр[en]](/images/005/702/5702879/13.jpg?rand=916744)
-
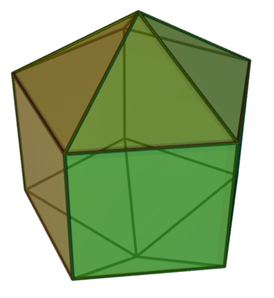
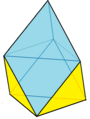 Скрученно удлинённая треугольная пирамида
Скрученно удлинённая треугольная пирамида -
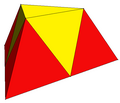 Триангулированный одноусечённый тетраэдр
Триангулированный одноусечённый тетраэдр -
![Удлинённый октаэдр[en]](/images/005/702/5702879/16.jpg?rand=214137)
-
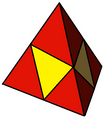 Триангулированный тетраэдр
Триангулированный тетраэдр -
 Наращенный треугольный купол
Наращенный треугольный купол -
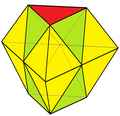 Триангулированная усечённая бипирамида
Триангулированная усечённая бипирамида -
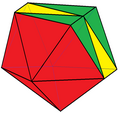 Восемнадцатигранник
Восемнадцатигранник -

-
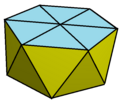
-

-

-
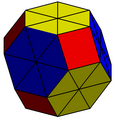
4.4.4.4
3.4.6.4:
-
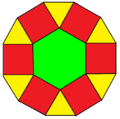 Шестиугольный купол
Шестиугольный купол
(вырожденный)
См. также
Примечания
- Craig S. Kaplan, George W. Hart. Bridges: Mathematical Connections in Art, Music and Science. — 2001.
Ссылки
- от 16 июля 2012 на Wayback Machine
- от 2 мая 2014 на Wayback Machine
- 2020-09-11
- 1