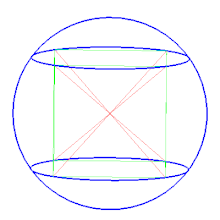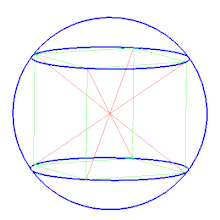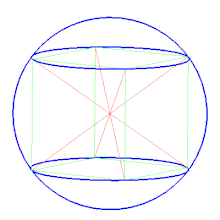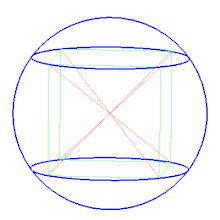
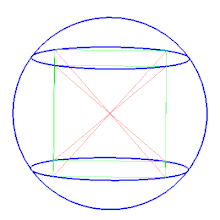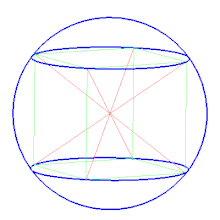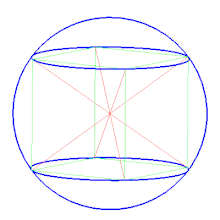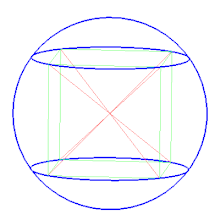
Описанная сфера — сфера, содержащая внутри себя многогранник, все вершины которого лежат на сфере. В двумерном случае описанная сфера представляет собой описанную окружность .

Существование

Если такая сфера существует, она не обязательно является наименьшей содержащей многогранник сферой. Например, тетраэдр , образованный вершиной куба и тремя её соседями, обладает той же описанной сферой, что и куб, но данный тетраэдр можно поместить в меньшую сферу, в которой три соседние вершины будут лежать на экваторе. Наименьшая сфера, содержащая данный многогранник, является описанной сферой для выпуклой оболочки подмножества вершин многогранника.

Связанные понятия

Описанная сфера является трёхмерным аналогом описанной окружности. Все правильные многогранники обладают описанными сферами, но большинство неправильных многогранников не имеет описанных сфер, поскольку в общем случае не все вершины могут лежать на одной сфере. Описанная сфера (при её наличии) является примером ограничивающей сферы . Для любого многогранника можно определить наименьшую ограничивающую сферу.

Среди других сфер, определяемых для некоторых многогранников, можно отметить полувписанную сферу , касающуюся всех рёбер многогранника, и вписанную сферу , касающуюся всех граней многогранника. Для правильных многогранников все три сферы существуют и являются концентрическими.

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .