Полная стоимость кредита
- 1 year ago
- 0
- 0
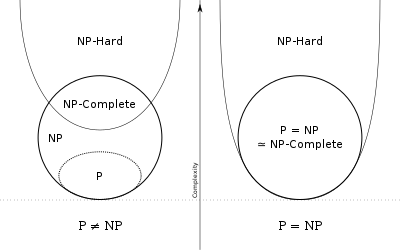

NP-полная задача — в теории алгоритмов задача с ответом «да» или «нет» из класса NP , к которой можно свести любую другую задачу из этого класса за полиномиальное время (то есть при помощи операций, число которых не превышает некоторого полинома в зависимости от размера исходных данных). Таким образом, NP-полные задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них будет найден «полиномиально быстрый» алгоритм решения, то и любую другую задачу из класса NP можно будет решить так же «быстро».
Алфавитом называется всякое конечное множество символов (например, { } или { }). Множество всех возможных слов (конечных строк , составленных из символов этого алфавита) над некоторым алфавитом обозначается . Языком над алфавитом называется всякое подмножество множества , то есть .
Задачей распознавания для языка называется определение того, принадлежит ли данное слово языку .
Пусть и — два языка над алфавитом . Язык называется сводимым (по Карпу) к языку , если существует функция , , вычислимая за полиномиальное время , обладающая следующим свойством:
Язык называется NP-трудным , если любой язык из класса NP сводится к нему. Язык называют NP-полным , если он NP-труден, и при этом сам лежит в классе NP.
Неформально говоря, то что задача сводится к задаче , означает, что задача «не сложнее» задачи (так как, если мы можем решить , то можем решить и ). Таким образом, класс NP-трудных задач включает NP-полные задачи и задачи, которые «сложнее» их (то есть те задачи, к которым могут быть сведены NP-полные задачи). Класс NP включает NP-полные задачи и задачи, которые «легче» их (то есть те задачи, которые сводятся к NP-полным задачам).
Из определения следует, что, если будет найден алгоритм, решающий некоторую (любую) NP-полную задачу за полиномиальное время, то все NP-задачи окажутся в классе P , то есть будут решаться за полиномиальное время.
Задача называется NP-полной в сильном смысле , если у неё существует подзадача, которая:
Класс таких задач называется NPCS . Если гипотеза P ≠ NP верна, то для NPCS-задачи не существует псевдополиномиального алгоритма [ источник не указан 2376 дней ] .
Вопрос о совпадении классов P и NP уже более тридцати лет является одной из центральных открытых проблем . Научное сообщество склоняется к отрицательному ответу на этот вопрос — в этом случае решать NP-полные задачи за полиномиальное время не удастся.