Кусочно-гладкая функция
- 1 year ago
- 0
- 0
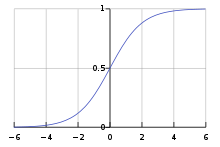
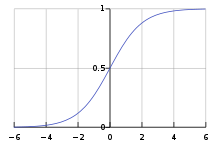
В искусственных нейронных сетях функция активации нейрона определяет выходной сигнал, который определяется входным сигналом или набором входных сигналов. Стандартная компьютерная микросхема может рассматриваться как цифровая сеть функций активации, которые могут принимать значения «ON» (1) или «OFF» (0) в зависимости от входа. Это похоже на поведение линейного перцептрона в нейронных сетях . Однако только нелинейные функции активации позволяют таким сетям решать нетривиальные задачи с использованием малого числа узлов. В искусственных нейронных сетях эта функция также называется передаточной функцией .
В биологических нейронных сетях функция активации обычно является абстракцией, представляющей скорость возбуждения потенциала действия в клетке . В наиболее простой форме эта функция является двоичной — то есть нейрон либо возбуждается, либо нет. Функция выглядит как , где — ступенчатая функция Хевисайда . В этом случае нужно использовать много нейронов для вычислений за пределами линейного разделения категорий.
Прямая с положительным угловым коэффициентом может быть использована для отражения увеличения скорости возбуждения по мере увеличения входного сигнала. Такая функция имела бы вид , где — наклон прямой . Эта функция активации линейна, а потому имеет те же проблемы, что и двоичная функция. Кроме того, сети, построенные с использованием такой модели, имеют , поскольку возбуждение приоритетных входов нейронов стремится к безграничному увеличению, так как эта функция не .
Все проблемы, упомянутые выше, можно решить с помощью нормализуемой сигмоидной функции активации. Одна из реалистичных моделей остаётся в нулевом состоянии, пока не придёт входной сигнал, в этот момент скорость возбуждения сначала быстро возрастает, но постепенно достигает асимптоты в 100 % скорости возбуждения. Математически, это выглядит как , где гиперболический тангенс можно заменить любой сигмоидой . Такое поведение реально имеет место в биологическом нейроне, поскольку нейроны не могут физически возбуждаться быстрее некоторой определённой скорости. Эта модель, однако, имеет несколько проблем в вычислительных сетях , поскольку функция не дифференцируема , что нужно для вычисления обратной передачи ошибки обучения .
Последняя модель, которая используется в многослойных перцептронах — сигмоидная функция активации в форме гиперболического тангенса. Обычно используются два вида этой функции: , образ которой нормализован к интервалу [-1, 1], и , сдвинутая по вертикали для нормализации от 0 до 1. Последняя модель считается более биологически реалистичной, но имеет теоретические и экспериментальные трудности с вычислительными ошибками некоторых типов.
Специальный класс функций активации, известный как радиальные базисные функции (РБФ) используются в РБФ сетях , которые крайне эффективны в качестве универсальных аппроксиматоров функций. Эти функции активации могут принимать множество форм, но обычно берётся одна из следующих трёх функций:
где является вектором, представляющим центр функции, а и являются параметрами, влияющими на расходимость радиуса.
Методы опорных векторов (SVM) могут эффективно использовать класс функций активации, который включает как сигмоиды, так и РБФ. В этом случае вход преобразуется для отражения гиперплоскости границы решений основываясь на нескольких обучающих входных данных, называемых опорными векторами . О функции активации для закрытого уровня этих машин говорят как о ядре скалярного произведения ( англ. inner product kernel ), . Опорные вектора представляются как центры в РБФ с ядром, равным функции активации, но они принимают единственный вид в перцептроне
где для сходимости и должны удовлетворять некоторым условиям. Эти машины могут принимать полиномиальные функции активации любого порядка
Функции активации бывают следующих типов:
Некоторые желательные свойства функций активации:
Следующая таблица сравнивает свойства некоторых функций активации, которые являются функциями одной свёртки x от предыдущего уровня или уровней:
| Название | График | Уравнение | Производная (по x ) | Область значений | Порядок гладкости | Монотонная | Монотонная производная |
Аппроксимирует тождественную
функцию около начала координат |
|---|---|---|---|---|---|---|---|---|
| Тождественная |

|
Да | Да | Да | ||||
| Единичная ступенька |

|
Да | Нет | Нет | ||||
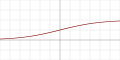
| Логистическая (сигмоида или Гладкая ступенька) |
|
[1] | Да | Нет | Нет | |||
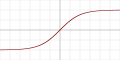
| th |
|
Да | Нет | Да | ||||
| arctg |
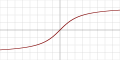
|
Да | Нет | Да | ||||
| Softsign |
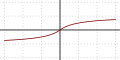
|
Да | Нет | Да | ||||
| Обратный квадратный корень ( англ. Inverse square root unit , ISRU) |
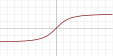
|
Да | Нет | Да | ||||
|
(или Полулинейный элемент)
( англ. Rectified linear unit , ReLU) |
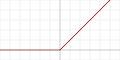
|
Да | Да | Нет | ||||
| Линейный выпрямитель с «утечкой» ( англ. Leaky rectified linear unit , Leaky ReLU) |
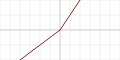
|
Да | Да | Нет | ||||
| Параметрический линейный выпрямитель ( англ. Parameteric rectified linear unit , PReLU) |
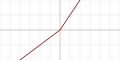
|
[2] |
Да,
когда |
Да |
Да,
когда |
|||
| Рандомизированный линейный выпрямитель с «утечкой» ( англ. Randomized leaky rectified linear unit , RReLU) |
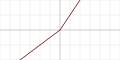
|
[3] | Да | Да | Нет | |||
| Экспоненциальная линейная функция ( англ. Exponential linear unit , ELU) |
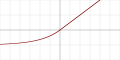
|
Да,
когда |
Да,
когда |
Да,
когда |
||||
| Масштабированная экспоненциальная линейная функция ( англ. Scaled exponential linear unit , SELU) |
с и |
Да | Нет | Нет | ||||
| Линейный S-выпрямитель ( англ. S-shaped rectified linear activation unit , SReLU) |
являются параметрами. |
Нет | Нет | Нет | ||||
| Обратный квадратный линейный корень ( англ. Inverse square root linear unit , ISRLU) |
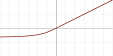
|
Да | Да | Да | ||||
| Адаптивная кусочно-линейная функция ( англ. Adaptive piecewise linear , APL) | [4] | Нет | Нет | Нет | ||||
| SoftPlus |
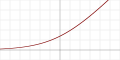
|
Да | Да | Нет | ||||
| Выгнутая тождественная функция ( англ. Bent identity ) |
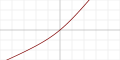
|
Да | Да | Да | ||||
| Cигмоидно-взвешенная линейная функция ( англ. Sigmoid-weighted linear unit , SiLU) | [5] | [6] | Нет | Нет | Нет | |||
| SoftExponential |

|
Да | Да |
Да,
когда |
||||
| Синусоида |
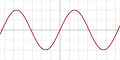
|
Нет | Нет | Да | ||||
| Sinc |
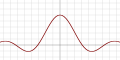
|
Нет | Нет | Нет | ||||
| Гауссова |

|
Нет | Нет | Нет |
Следующая таблица перечисляет функции активации, которые не являются функциями от одной свёртки x от предыдущего уровня или уровней:
| Название | Уравнение | Производные | Область значений | Степень гладкости |
|---|---|---|---|---|
| Softmax | для i = 1, …, J | [7] | ||
| Maxout |
Здесь обозначает символ Кронекера .