Алгоритм Ву — алгоритм разложения отрезка в растр со сглаживанием . Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхэма без сглаживания.

Предложен У Сяолинем ( Xiaolin Wu , отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом ( ) в июле 1991 года.

Алгоритм

Горизонтальные и вертикальные линии не требуют никакого сглаживания, поэтому их рисование выполняется отдельно. Для остальных линий алгоритм Ву проходит их вдоль основной оси , подбирая координаты по неосновной оси аналогично алгоритму Брезенхема. Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является ${\displaystyle Ox}$ , то рассматриваются точки с координатами ${\displaystyle (x,y)}$ и ${\displaystyle (x,y+1)}$ . В зависимости от величины ошибки, которая показывает, как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше её интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всём её протяжении, создавая при этом иллюзию , что точки расположены вдоль линии не по две, а по одной.

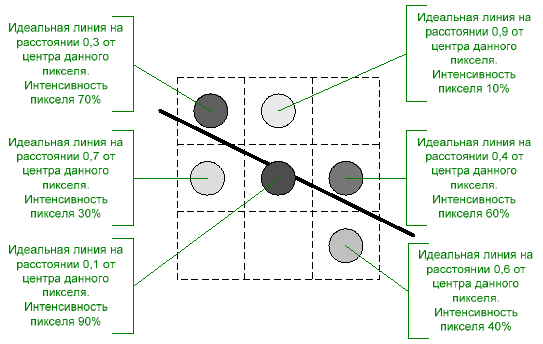
Реализация в псевдокоде (только для линии по оси ${\displaystyle Ox}$ ):

function plot(x, y, c) is
    // рисует точку с координатами (x, y)
    // и яркостью c (где 0 ≤ c ≤ 1)

function ipart(x) is
    return целая часть от x

function round(x) is
    return ipart(x + 0.5) // округление до ближайшего целого

function fpart(x) is
    return дробная часть x

function draw_line(x1,y1,x2,y2) is
   if x2 < x1 then
       swap(x1, x2)
       swap(y1, y2)
   end if
  
   dx:= x2 - x1
   dy := y2 - y1
   gradient:= dy ÷ dx
  
   // обработать начальную точку
   xend:= round(x1) 
   yend:= y1 + gradient × (xend - x1)
   xgapg:= 1 - fpart(x1 + 0.5)
   xpxl1:= xend  // будет использоваться в основном цикле
   ypxl1:= ipart(yend)
   plot(xpxl1, ypxl1, (1 - fpart(yend)) × xgap)
   plot(xpxl1, ypxl1 + 1, fpart(yend) × xgap)
   intery:= yend + gradient // первое y-пересечение для цикла
        
   // обработать конечную точку
   xend:= round(x2)
   yend:= y2 + gradient × (xend - x2)
   xgap:= fpart(x2 + 0.5)
   xpxl2:= xend  // будет использоваться в основном цикле
   ypxl2:= ipart(yend)
   plot(xpxl2, ypxl2, (1 - fpart(yend)) × xgap)
   plot(xpxl2, ypxl2 + 1, fpart(yend) × xgap)
     
   // основной цикл
   for x from xpxl1 + 1 to xpxl2 - 1 do
       plot(x, ipart(intery), 1 - fpart(intery))
       plot(x, ipart(intery) + 1, fpart(intery))
       intery := intery + gradient
   repeat
end function

Литература

• Майкл Абраш. (англ.) // Dr. Dobb's Journal : magazine. — июнь 1992. — Vol. 17 , no. 6 . — P. 139(7) . 1 марта 2010 года.
• У Сяолинь. (неопр.) // . — июль 1991. — Т. 25 , № 4 . — С. 143—152 .

См. также

• Алгоритмы построения отрезка
• Алгоритм Брезенхема
• Алгоритм DDA-линии
• ClearType
• Экранное сглаживание