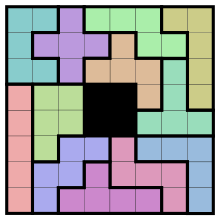
Полимино , или полиомино ( англ. polyomino ) — плоские геометрические фигуры, образованные путём соединения нескольких одноклеточных квадратов по их сторонам. Это полиформы , сегменты которых являются квадратами .

Фигуру полимино можно рассматривать как конечное связное подмножество бесконечной шахматной доски , которое может обойти ладья .

Названия полимино

Полимино ( n -мино) носят названия по числу n квадратов, из которых они состоят:

n	Название	n	Название
1	мономино	6	гексамино
2	домино	7	гептамино
3	тримино	8	октамино
4	тетрамино	9	нонамино или эннеомино
5	пентамино	10	декамино

История

Полимино использовались в занимательной математике по крайней мере с 1907 года , а известны были ещё в древности. Многие результаты с фигурами, содержащими от 1 до 6 квадратов, были впервые опубликованы в журнале «Fairy Chess Review» в период с 1937 по 1957 г., под названием «проблемы рассечения» ( англ. «dissection problems» ). Название «полимино» или «полиомино» ( англ. polyomino ) было придумано Соломоном Голомбом в 1953 году и затем популяризировано Мартином Гарднером .

В 1967 году журнал « Наука и жизнь » опубликовал серию статей о пентамино . В дальнейшем в течение ряда лет публиковались задачи, связанные с полимино и другими полиформами .

Обобщения полимино

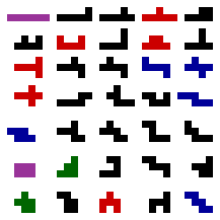
В зависимости от того, разрешается ли переворачивание или вращение фигур, различаются следующие три вида полимино :

• двусторонние полимино , или свободные полимино ( англ. free polyominoes ) — полимино, которые разрешается поворачивать и переворачивать;
• односторонние полимино ( англ. one-sided polyominoes ) — полимино, которые разрешается поворачивать в плоскости, но не разрешается переворачивать;
• фиксированные полимино ( англ. fixed polyominoes ) — полимино, которые не разрешается ни поворачивать, ни переворачивать.

В зависимости от условий связности соседних ячеек различаются :

• полимино — наборы квадратов, которые может обойти визирь ;
• псевдополимино , или полиплеты — наборы квадратов, которые может обойти король ;
• квазиполимино — произвольные наборы квадратов бесконечной шахматной доски.

В следующей таблице собраны данные о числе фигур полимино и его обобщений. Число квази- n -мино равно 1 при n = 1 и ∞ при n > 1.

n	полимино					псевдополимино
	двусторонние			односторонние	фиксированные	двусторонние	односторонние	фиксированные
	все	с отверстиями	без отверстий
1	1	0	1	1	1	1	1	1
2	1	0	1	1	2	2	2	4
3	2	0	2	2	6	5	6	20
4	5	0	5	7	19	22	34	110
5	12	0	12	18	63		166
6	35	0	35	60	216			3832
7	108	1	107	196		3031	5931	23 592
8		6			2725	18 770	37 196	147 941
9	1285	37	1248	2500	9910	118 133	235 456	940 982
10	4655		4460	9189	36 446	758 381	1 514 618	6 053 180
11	17 073		16 094	33 896	135 268	4 915 652	9 826 177	39 299 408
12	63 600	4 663	58 937	126 759	505 861	32 149 296	64 284 947	257 105 146

Полиформы

Полиформы — обобщение полимино, ячейками которого могут быть любые одинаковые многоугольники или многогранники. Иначе говоря, полиформа — плоская фигура или пространственное тело, состоящая из нескольких соединённых копий заданной основной формы .

Плоские (двумерные) полиформы включают в себя полиамонды , сформированные из равносторонних треугольников; полигексы , сформированные из правильных шестиугольников; полиаболо , состоящие из равнобедренных прямоугольных треугольников, и другие.

Примеры пространственных (трёхмерных) полиформ: поликубы, состоящие из трёхмерных кубов; полироны ( англ. polyrhons ), состоящие из ромбододекаэдров .

Полиформы также обобщаются на случай более высоких размерностей (например, сформированные из гиперкубов — полигиперкубы).

Задачи

Покрытия прямоугольников конгруэнтными полимино

Порядок полимино P — минимальное число конгруэнтных копий P , достаточное для того, чтобы сложить некоторый прямоугольник. Для полимино, из копий которых нельзя сложить ни одного прямоугольника, порядок не определён. Порядок полимино P равен 1 тогда и только тогда, когда P — прямоугольник .

Если существует хотя бы один прямоугольник, который можно покрыть нечётным числом конгруэнтных копий P , полимино P называется нечётным полимино ; если же прямоугольник можно сложить только из чётного числа копий P , P называется чётным полимино .

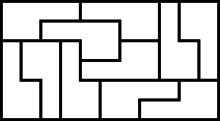
Эта терминология была введена в 1968 году .

Существует множество полимино порядка 2; примером являются так называемые L -полимино .

Полимино порядка 3 не существует; доказательство этого было опубликовано в 1992 году . Любое полимино, из трёх копий которого можно составить прямоугольник, само является прямоугольником и имеет порядок 1. Неизвестно, существует ли полимино, порядок которого — нечётное число, большее 3 .

Существуют полимино порядка 4 , 10 , 18 , 24 , 28 , 50 , 76 , 92 , ; существует конструкция, позволяющая получить полимино порядка 4 s для любого натурального s .

Кларнеру удалось найти непрямоугольное полимино порядка 2, из 11 копий которого можно составить прямоугольник , причём никакое ме́ньшее нечётное число копий этого полимино не может покрыть прямоугольник. На октябрь 2015 года неизвестно, существует ли непрямоугольное полимино, из 9, 7 или 5 копий которого можно составить прямоугольник; неизвестны также какие-либо другие примеры полимино с минимальной нечётной кратностью покрытия 11 (кроме найденного Кларнером).

Минимальные области

Минимальная область (англ. minimal region , minimal common superform ) для заданного набора полимино — полимино наименьшей возможной площади, содержащее каждое полимино из данного набора . Задача нахождения минимальной области для набора двенадцати пентамино была впервые поставлена Т. Р. Доусоном в журнале в 1942 году .

Для набора 12 пентамино существуют две минимальные девятиклеточные области, представляющие собой 2 из 1285 нонамино :

  ###     ###
#####    #####
  #       #

См. также

• Пентамино
• Полиамонды
• Полигексы
• Полиаболо
• Кубики сома
• Танграм

Примечания

Литература

• Голомб С.В. Полимино = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М. : Мир, 1975. — 207 с.
• Генри Э. Дьюдени. Кентерберийские головоломки = The Canterbury Puzzles and Other Curious Problems / Пер. с англ. Ю.Н.Сударева. — М. : Мир, 1979. — 353 с.
• Гарднер М. Математические головоломки и развлечения = Mathematical Puzzles and Diversions / Пер. с англ. Ю.А.Данилова. — М. : Мир, 1971. — 511 с.
• Гарднер М. Математические новеллы / Пер. с англ. Ю.А.Данилова. Под ред. Я.А.Смородинского. — М. : Мир, 1974. — 456 с.

Ссылки

• Антология Мартина Гарднера от 31 января 2014 на Wayback Machine
• Библиотека по математике от 9 ноября 2014 на Wayback Machine
• RSDN: Этюды для программистов от 10 ноября 2014 на Wayback Machine
• Хайдар Нурлигареев от 5 октября 2015 на Wayback Machine
• Michael Reid от 25 декабря 2018 на Wayback Machine
• Andrew Clarke The Poly Pages от 14 мая 2015 на Wayback Machine
• David Eppstein The Geometry Junkyard от 3 июля 2015 на Wayback Machine
• Miroslav Vicher от 15 октября 2015 на Wayback Machine
• Kevin L. Gong от 3 мая 2015 на Wayback Machine