Interested Article - Бордизм

- 2021-05-05
- 1
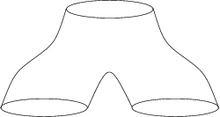
Бордизм , также бордантность — термин топологии , употребляющийся самостоятельно или в составе стандартных словосочетаний в нескольких родственных смыслах, почти во всех из них вместо бордизм раньше [ источник не указан 3754 дня ] говорили о кобордизмах , старая терминология тоже сохранилась.
Неориентированные бордизмы
Неориентированные бордизмы — простейший вариант бордизмов. Два гладких замкнутых -мерных многообразия и бордантны (ограничивают, или внутренне гомологичны), если существует гладкое компактное -мерное многообразие (называемое плёнка ), край которого состоит из двух многообразий и , (или точнее многообразий и диффеоморфных, соответственно, и посредством некоторых диффеоморфизмов и ). Совокупность многообразий, бордантных друг другу, называется классами бордизмов , а тройку называют бордизмом (точнее было бы говорить о пятёрке ).
Множество классов бордизмов -мерных многообразий образует абелеву группу относительно несвязного объединения , называемую группой бордизмов . Нулем в ней служит класс бордизмов, состоящих из многообразий, которые являются границей некоторого многообразия (другие названия: — ограничивающее многообразие , — внутренне гомологично , или бордантно нулю). Элементом обратным данному классу бордизмов, является сам этот класс (так как объединение двух копий диффеоморфно границе прямого произведения ). Прямая сумма групп является коммутативным градуированным кольцом , умножение в котором индуцировано прямым произведением многообразий, с единицей, заданной классом бордизмов точки.
Бордизмы с дополнительной структурой
Ориентированные бордизмы
Ориентированные бордизмы — наиболее простой тип бордизмов гладких замкнутых многообразий с дополнительной структурой. Два ориентированных многообразия и ориентированно бордантны , если они бордантны в прежнем смысле, причём плёнка ориентирована, и (в прежних обозначениях) ориентация, индуцированная ориентацией на и (как на частях края), переходит при диффеоморфизмах и , соответственно, в исходную ориентацию и в ориентацию, противоположную исходной ориентации . Аналогично , и вводятся группы ориентированных бордизмов и кольцо .
Другие варианты
Другие варианты бордизмов многообразий с дополнительной структурой — очень важные бордизмы квазикомплексных многообразий (называемые также унитарными бордизмами), бордизмы многообразий, на которых действует группа преобразований, -бордизмы. Имеются также варианты несколько иного рода, для кусочно линейных или топологических многообразий, для комплексов Пуанкаре и т. д. Особое положение занимают бордизмы слоений и (ранее называемые -эквивалентностями); последние служат для связи дифференциальной и гомотопической топологии.
Свойства
- Два многообразия бордантны, тогда и только тогда, когда у них совпадают характеристические числа ( числа Штифеля — Уитни в неориентируемом случае и числа Штифеля — Уитни и числа Понтрягина — в ориентируемом).
История
Первый пример — бордизм оснащённых многообразий , введённый в 1938 году Понтрягиным , который показал, что классификация этих бордизмов эквивалентна вычислению гомотопических групп сфер , и таким путём смог найти и . Неориентированные и ориентированные бордизмы были введены в 1951—53 годах Рохлиным , вычислившим для . Понтрягин доказал, что если два многообразия бордантны, то у них совпадают характеристические числа . Впоследствии оказалось, что обратное тоже верно.
Литература
- Милнор Дж., Уоллес А. Дифференциальная топология / Пер. с англ. — М. : Мир, 1972. — 280 с.
См. также
- 2021-05-05
- 1





















![{\displaystyle M\times [0,\;1]}](/images/005/741/5741458/23.jpg?rand=583490)
























