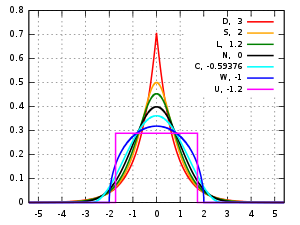
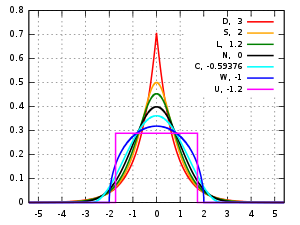
Несколько распределений и их коэффициенты эксцесса. В порядке уменьшения высоты пика (значения в нуле):
распределение Лапласа
;
(англ.)
(
;
Логистическое распределение
;
Нормальное распределение
;
(англ.)
(
;
Полукруговой закон Вигнера
;
Равномерное распределение
Коэффицие́нт эксце́сса
(коэффициент островершинности) в
теории вероятностей
— мера остроты пика
распределения
случайной величины.
Определение
Пусть задана
случайная величина
X
{\displaystyle X}
, такая что
E
|
X
|
4
<
∞
{\displaystyle \mathbb {E} |X|^{4}<\infty }
. Пусть
μ
4
{\displaystyle \mu _{4}}
обозначает четвёртый
центральный момент
:
μ
4
=
E
[
(
X
−
E
X
)
4
]
{\displaystyle \mu _{4}=\mathbb {E} \left[(X-\mathbb {E} X)^{4}\right]}
, а
σ
=
D
[
X
]
{\displaystyle \sigma ={\sqrt {\mathrm {D} [X]}}}
—
стандартное отклонение
X
{\displaystyle X}
. Тогда коэффициент эксцесса задаётся формулой:
γ
2
=
μ
4
σ
4
−
3
{\displaystyle \gamma _{2}={\frac {\mu _{4}}{\sigma ^{4}}}-3}
.
Замечание
Свойства коэффициента эксцесса
γ
2
∈
[
−
2
,
∞
)
{\displaystyle \gamma _{2}\in [-2,\infty )}
.
Пусть
X
1
,
…
,
X
n
{\displaystyle X_{1},\ldots ,X_{n}}
—
независимые
случайные величины с равной
дисперсией
. Пусть
Y
=
∑
i
=
1
n
X
i
{\displaystyle Y=\sum \limits _{i=1}^{n}X_{i}}
. Тогда
γ
2
,
Y
=
1
n
2
∑
i
=
1
n
γ
2
,
X
i
{\displaystyle \gamma _{2,Y}={\frac {1}{n^{2}}}\sum \limits _{i=1}^{n}\gamma _{2,X_{i}}}
,
где
γ
2
,
Y
,
γ
2
,
X
i
,
i
=
1
,
…
,
n
{\displaystyle \gamma _{2,Y},\gamma _{2,X_{i}},\;i=1,\ldots ,n}
— коэффициенты эксцесса соответствующих случайных величин.
См. также