Interested Article - Двудольный граф
- 2020-01-20
- 1

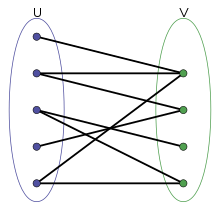
Двудо́льный граф или бигра́ф в теории графов — это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет вершину из одной части с какой-то вершиной другой части, то есть не существует рёбер между вершинами одной и той же части графа.
Определение

Граф называется двудольным, если множество его вершин можно разбить на две части так, что:
- ни одна вершина в не соединена с вершинами в ;
- ни одна вершина в не соединена с вершинами в .
В этом случае, подмножества вершин и называются долями двудольного графа .
Связанные определения
Двудольный граф называется полным двудольным (это понятие отлично от полного графа ; то есть, такого, в котором каждая пара вершин соединена ребром), если для каждой пары вершин существует ребро . Для
такой граф обозначается символом .
Примеры
Примеры двудольных графов:
- любое дерево является двудольным графом;
- любой простой цикл, состоящий из чётного числа вершин;
- любой планарный граф , у которого каждая грань ограничена чётным количеством ребер.
Двудольные графы естественно возникают при моделировании отношений между двумя различными классами объектов. К примеру граф футболистов и клубов: ребро соединяет соответствующего игрока и клуб, если игрок играл в этом клубе.
Двудольные графы используют для описания LDPC кодов.
Свойства
-
Граф является двудольным тогда и только тогда, когда он не содержит
цикла
нечётной
длины.
- В частности двудольный граф не может содержать клику размером более 2.
- Граф является двудольным тогда и только тогда, когда он 2-хроматический; то есть его хроматическое число равняется двум.
- Граф разбивается на пары разноцветных вершин тогда и только тогда, когда любые элементов одной из долей связаны по крайней мере с элементами другой ( Теорема о свадьбах ).
- Полный двудольный граф, у которого в каждой части больше 2 вершин, является непланарным .
- Любой двудольный граф является совершенным .
Проверка двудольности

Для того, чтобы проверить граф на предмет двудольности, достаточно в каждой компоненте связности выбрать любую вершину и помечать оставшиеся вершины во время обхода графа (например, поиском в ширину ) поочерёдно как чётные и нечётные (см. иллюстрацию). Если при этом не возникнет конфликта, все чётные вершины образуют множество , а все нечётные — .
Применения
- Сети Петри
- Граф Леви
- Теория кодирования
См. также
Ссылки
- Hazewinkel, Michiel, ed. (2001), , Encyclopedia of Mathematics , Springer , ISBN 978-1-55608-010-4
- :
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- 2020-01-20
- 1

























