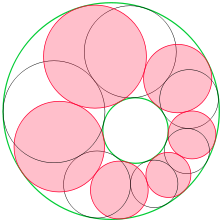
Поризм Штейнера : Рассмотрим цепочку окружностей ${\displaystyle S_{1},S_{2},\ldots ,S_{n}}$ , каждая из которых касается двух соседних ( ${\displaystyle S_{n}}$ касается ${\displaystyle S_{n+1}}$ и ${\displaystyle S_{n-1}}$ ) и двух данных непересекающихся окружностей ${\displaystyle R_{1}}$ и ${\displaystyle R_{2}}$ . Тогда для любой окружности ${\displaystyle T_{1}}$ , касающейся ${\displaystyle R_{1}}$ и ${\displaystyle R_{2}}$ (одинаковым образом, если ${\displaystyle R_{1}}$ и ${\displaystyle R_{2}}$ не лежат одна в другой, внешним и внутренним образом — в противном случае), существует аналогичная цепочка из ${\displaystyle n}$ касающихся окружностей ${\displaystyle T_{1},T_{2},\ldots ,T_{n}}$ .

Доказывается применением инверсии , которая переводит пару окружностей ${\displaystyle R_{1}}$ и ${\displaystyle R_{2}}$ в концентрические.

См. также

• Поризм Понселе
• Круги Форда
• Цепь Паппа Александрийского

Литература

• Коксетер Г. С. М. , Грейтцер С. П. . — М. : Наука , 1978. — Т. 14. — ( Библиотека математического кружка ).