Простое число
- 1 year ago
- 0
- 0

Наибольшее известное простое число — 2 82 589 933 − 1 . Оно было найдено Патриком Ларошем в рамках проекта GIMPS 7 декабря 2018 года и содержит 24 862 048 десятичных цифр .
Согласно теореме Евклида , количество простых чисел бесконечно. Следовательно, количество простых чисел, превышающих наибольшее известное на данный момент, тоже бесконечно. Многочисленные энтузиасты, в том числе некоторые учёные-математики, занимаются поиском рекордных по величине простых чисел. За их нахождение организацией Electronic Frontier Foundation было предложено несколько наград в зависимости от величины числа. Так, в 2009 году была вручена премия размером в 100 000 долларов США, назначенная сообществом Electronic Frontier Foundation за нахождение простого числа, десятичная запись которого содержит не менее 10 миллионов цифр.
Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа. Один из рекордов поставил в 1772 году Эйлер , доказав, что число Мерсенна 2 31 − 1 = 2 147 483 647 — простое .
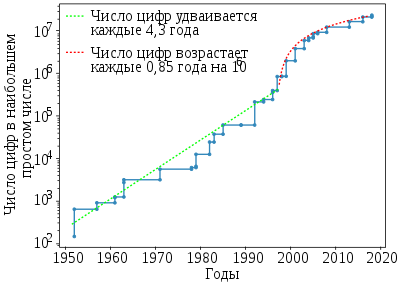
Быстрейшим из известных тестов простоты является тест Люка — Лемера для чисел Мерсенна , реализованный с использованием быстрого преобразования Фурье . В связи с этим большинство из обнаруженных в последнее время больших простых чисел — числа Мерсенна. Последние восемнадцать чисел, на момент открытия ставших рекордными по величине из известных простых чисел — также числа Мерсенна .
Рекорд принадлежит простому числу 2 82 589 933 − 1 , найденному в рамках проекта GIMPS 7 декабря 2018 года. Десятичная запись числа имеет длину 24 862 048 цифр. Об успешном доказательстве простоты числа было объявлено 21 декабря 2018 года .
В таблице ниже представлены наибольшие известные простые числа в порядке нахождения. Числа Мерсенна с показателем n обозначены M n = 2 n − 1.
| Число | Количество десятичных цифр | Год нахождения |
|---|---|---|
| M 13 | 4 | 1456 |
| M 17 | 6 | 1460 |
| M 19 | 6 | 1588 |
| M 31 | 10 | 1772 |
| M 127 | 39 | 1876 |
| 180×(M 127 ) 2 + 1 | 79 | 1951 |
| M 521 | 157 | 1952 |
| M 607 | 183 | 1952 |
| M 1279 | 386 | 1952 |
| M 2203 | 664 | 1952 |
| M 2281 | 687 | 1952 |
| M 3217 | 969 | 1957 |
| M 4423 | 1332 | 1961 |
| M 9689 | 2917 | 1963 |
| M 9941 | 2993 | 1963 |
| M 11 213 | 3376 | 1963 |
| M 19 937 | 6002 | 1971 |
| M 21 701 | 6533 | 1978 |
| M 23 209 | 6987 | 1979 |
| M 44 497 | 13 395 | 1979 |
| M 86 243 | 25 962 | 1982 |
| M 132049 | 39 751 | 1983 |
| M 216 091 | 65 050 | 1985 |
| 391 581⋅2 216 193 − 1 | 65 087 | 1989 |
| M 756 839 | 227 832 | 1992 |
| M 859 433 | 258 716 | 1994 |
| M 1 257 787 | 378 632 | 1996 |
| M 1 398 269 | 420 921 | 1996 |
| M 2 976 221 | 895 932 | 1997 |
| M 3 021 377 | 909 526 | 1998 |
| M 6 972 593 | 2 098 960 | 1999 |
| M 13 466 917 | 4 053 946 | 2001 |
| M 20 996 011 | 6 320 430 | 2003 |
| M 24 036 583 | 7 235 733 | 2004 |
| M 25 964 951 | 7 816 230 | 2005 |
| M 30 402 457 | 9 152 052 | 2005 |
| M 32 582 657 | 9 808 358 | 2006 |
| M 43 112 609 | 12 978 189 | 2008 |
| M 57 885 161 | 17 425 170 | 2013 |
| M 74 207 281 | 22 338 618 | 2016 |
| M 77 232 917 | 23 249 425 | 2017 |
| M 82 589 933 | 24 862 048 | 2018 |
| Место | Число | Первооткрыватель | Дата нахождения | Количество цифр | Источник |
|---|---|---|---|---|---|
| 1 | 2 82 589 933 − 1 | GIMPS | 7 декабря 2018 | 24 862 048 | |
| 2 | 2 77 232 917 − 1 | GIMPS | 26 декабря 2017 | 23 249 425 | |
| 3 | 2 74 207 281 − 1 | GIMPS | 7 января 2016 | 22 338 618 | |
| 4 | 2 57 885 161 − 1 | GIMPS | 25 января 2013 | 17 425 170 | |
| 5 | 2 43 112 609 − 1 | GIMPS | 23 августа 2008 | 12 978 189 | |
| 6 | 2 42 643 801 − 1 | GIMPS | 12 апреля 2009 | 12 837 064 | |
| 7 | 2 37 156 667 − 1 | GIMPS | 6 сентября 2008 | 11 185 272 | |
| 8 | 2 32 582 657 − 1 | GIMPS | 4 сентября 2006 | 9 808 358 | |
| 9 | 10 223×2 31 172 165 + 1 | PrimeGrid | 6 ноября 2016 | 9 383 761 | |
| 10 | 2 30 402 457 − 1 | GIMPS | 15 декабря 2005 | 9 152 052 |
|
|
В другом языковом разделе
есть более полная статья
(англ.)
.
|