Группа восьми (художественная группа)
- 1 year ago
- 0
- 0

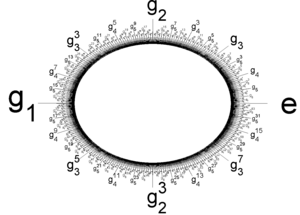
Квазициклическая p -группа , для фиксированного простого числа p — это единственная p -группа , в которой из любого элемента можно извлечь ровно p корней p -й степени. Обычно обозначается как Z ( p ∞ )
Квазициклическую p -группу также её называют p -группой Прюфера , в честь немецкого математика Хайнца Прюфера .
Квазициклическая p -группа может быть представлена как подгруппа U(1) , состоящая из комплексных корней из единицы степени p n , где n пробегает все натуральные числа:
Эквивалентным образом, квазициклическую p -группу можно рассматривать как подгруппу Q/Z , состоящую из элементов, порядок которых является степенью p :
Также p -группа Прюфера может быть задана образующими и соотношениями:
Квазициклическая p -группа — это единственная бесконечная p -группа, являющаяся (то есть такой, что любое конечное подмножество её элементов порождает циклическую группу ). Нетрудно видеть, что все собственные подгруппы квазициклической группы являются циклическими.
Квазициклическая группа является делимой .
В теории локально компактных топологических групп квазициклическая p -группа, снабжённая дискретной топологией , является двойственной по Понтрягину к компактной группе целых p -адических чисел .
Квазициклические p -группы, для всевозможных простых p — это единственные бесконечные группы, такие что множество их подгрупп линейно упорядочено по вложению:
На этой цепочке включений p -группа Прюфера представлена как прямой предел своих конечных подгрупп.
Как -модуль, p -группа Прюфера является артиновой , но не является нётеровой (аналогично, она является артиновой , но не нётеровой группой). В таком качестве она является контрпримером к возможному утверждению о том, что любой артинов модуль нётеров.