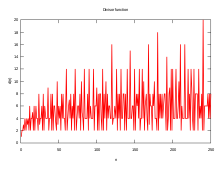
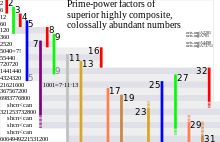
В математике весьма суперсоставное число — это натуральное число , которое имеет больше делителей , чем любое другое число, масштабируемое относительно некоторой положительной степени самого числа . Это более сильное ограничение, чем ограничение сверхсоставного числа , которое определяется как имеющее больше делителей, чем любое меньшее положительное целое число .

Перечислены первые 10 весьма суперсоставных чисел и их факторизация .

# простые множители	ВССЧ n	простая факторизация	простые показатели степени	# делители d( n )		праймориал факторизация
1	2	2	1	2	2	2
2	6	2 ⋅ 3	1,1	2 2	4	6
3	12	2 2 ⋅ 3	2,1	3×2	6	2 ⋅ 6
4	60	2 2 ⋅ 3 ⋅ 5	2,1,1	3×2 2	12	2 ⋅ 30
5	120	2 3 ⋅ 3 ⋅ 5	3,1,1	4×2 2	16	2 2 ⋅ 30
6		2 3 ⋅ 3 2 ⋅ 5	3,2,1	4×3×2	24	2 ⋅ 6 ⋅ 30
7		2 3 ⋅ 3 2 ⋅ 5 ⋅ 7	3,2,1,1	4×3×2 2	48	2 ⋅ 6 ⋅ 210
8	5040	2 4 ⋅ 3 2 ⋅ 5 ⋅ 7	4,2,1,1	5×3×2 2	60	2 2 ⋅ 6 ⋅ 210
9		2 4 ⋅ 3 2 ⋅ 5 ⋅ 7 ⋅ 11	4,2,1,1,1	5×3×2 3	120	2 2 ⋅ 6 ⋅ 2310
10		2 4 ⋅ 3 2 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 13	4,2,1,1,1,1	5×3×2 4	240	2 2 ⋅ 6 ⋅ 30030

Для весьма суперсоставного числа n существует положительное действительное число ε такое, что для всех натуральных чисел k , меньших n , мы имеем

${\displaystyle {\frac {d(n)}{n^{\varepsilon }}}\geq {\frac {d(k)}{k^{\varepsilon }}}}$

и для всех натуральных чисел k , больших n , имеем

${\displaystyle {\frac {d(n)}{n^{\varepsilon }}}>{\frac {d(k)}{k^{\varepsilon }}}}$

где d(n) , функция делителей , обозначает количество делителей числа n . Термин был введён Рамануджаном ( 1915 год ) .

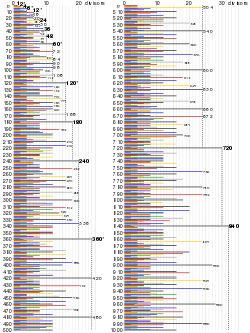
Первые 15 весьма суперсоставных чисел 2 , 6 , 12 , 60 , 120 , , , 5040 , 55440, 720720, 1441440, 4324320, 21621600, 367567200, 6983776800 (последовательность в OEIS ) также являются первыми 15 колоссально избыточными числами , которые удовлетворяют аналогичному условию, основанному на функции суммы делителей, а не на числе делителей.

Свойства

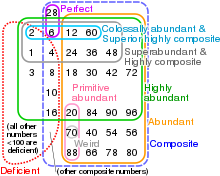
Все весьма суперсоставные числа являются сверхсоставными .

Эффективное построение множества всех весьма суперсоставных чисел даётся следующим монотонным отображением положительных действительных чисел . Пусть

${\displaystyle e_{p}(x)=\left\lfloor {\frac {1}{{\sqrt[{x}]{p}}-1}}\right\rfloor \quad }$

для любого простого числа p и положительного действительного x . Тогда

${\displaystyle \quad s(x)=\prod _{p\in \mathbb {P} }p^{e_{p}(x)}\quad }$ является весьма суперсоставным числом.

Обратите внимание, что произведение не нужно вычислять бесконечно, потому что если ${\displaystyle p>2^{x}}$ , тогда ${\displaystyle e_{p}(x)=0}$ , поэтому произведение для расчёта ${\displaystyle s(x)}$ может быть прекращено при ${\displaystyle p\geq 2^{x}}$ .

Также обратите внимание, что в определении ${\displaystyle e_{p}(x)}$ , ${\displaystyle 1/x}$ аналогично ${\displaystyle \varepsilon }$ в неявном определении весьма суперсоставного числа.

Более того, для каждого весьма суперсоставного числа ${\displaystyle s^{\prime }}$ существует полуоткрытый интервал ${\displaystyle I\subset \mathbb {R} ^{+}}$ такой, что ${\displaystyle \forall x\in I:s(x)=s^{\prime }}$ .

Из этого представления следует, что существует бесконечная последовательность ${\displaystyle \pi _{1},\pi _{2},\ldots \in \mathbb {P} }$ такая, что для n -го весьма суперсоставного числа ${\displaystyle s_{n}}$ содержит

${\displaystyle s_{n}=\prod _{i=1}^{n}\pi _{i}}$

Первыми ${\displaystyle \pi _{i}}$ являются 2, 3, 2, 5, 2, 3, 7, ... (последовательность в OEIS ). Другими словами, частное двух последовательных весьма суперсоставных чисел является простым числом .

Весьма суперсоставные корни

Первые несколько весьма суперсоставных чисел часто использовались как основание системы счисления из-за их высокой делимости по размеру. Например:

• Двоичное (основание 2)
• (основание 6)
• Двенадцатеричное (основание 12)
• Шестидесятеричное (основание 60)

Более крупные весьма суперсоставные числа можно использовать и по-другому. Число 120 отображается как длинная сотня , а число 360 — как число градусов в круге.

Примечания

Ссылки

• Ramanujan, S. (1915). (PDF) . Proc. London Math. Soc . Series 2. 14 : 347—409. doi : . JFM . Reprinted in Collected Papers (Ed. G. H. Hardy et al.), New York: Chelsea, pp. 78–129, 1962
• Handbook of number theory I. — Dordrecht : Springer-Verlag , 2006. — P. 45–46. — ISBN 1-4020-4215-9 .

Внешние ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .