Энтропия
- 1 year ago
- 0
- 0
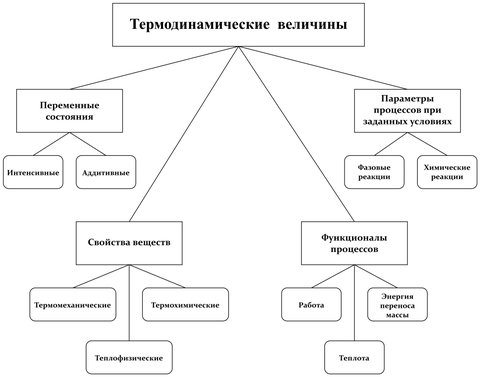
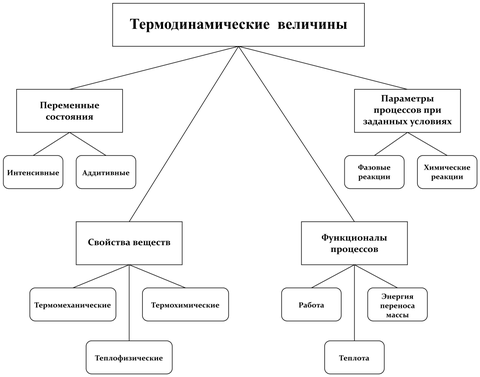
Термодинамическая функция состояния — это физическая величина, рассматриваемая как функция нескольких независимых переменных состояния. Причём набор независимых переменных выбирается из требования необходимости и достаточности для полного описания мгновенного состояния однородной термодинамической системы. Функции состояния заданы для текущего состояния равновесия системы . Их применяют для термодинамического описания сплошных сред — газов , жидкостей , твёрдых веществ , включая кристаллы , эмульсии и чернотельное излучение . Функции состояния не зависят от пути термодинамического процесса, по которому система достигла своего нынешнего состояния. Термодинамическая функция состояния описывает состояние равновесия системы и, следовательно, также описывает тип системы. Например, функция состояния может описывать газ, жидкость или твердую фазу; гетерогенную или гомогенную смесь; и количество энергии, необходимое для создания таких систем или перевода их в другое состояние равновесия. Следует уточнить, что если равновесие наступает не во всём объёме системы, а только в её бесконечно малой части, то термодинамические функции состояния также описывают эти малые части, а изменение термодинамических переменных состояния определены как функции времени и координаты, которые меняются благодаря потокам в среде, стремящихся привести в равновесное состояние всю систему. Понятие о локальности термодинамического равновесия позволяет использовать термодинамические функции состояния в неравновесной термодинамике.
Например, внутренняя энергия , энтальпия и энтропия являются величинами состояния, потому что они количественно описывают состояние равновесия термодинамической системы , независимо от того, как система пришла в это состояние. Напротив, механическая работа и тепло — это величины зависящие от процесса или функции пути, потому что их значения зависят от конкретного перехода (или пути) между двумя состояниями термодинамического равновесия. Тепло в определённых дискретных количествах может описывать определённую функцию состояния, такую как энтальпия, но в целом не описывает систему в действительности, если только она не определена как функция состояния определённой системы, и, таким образом, энтальпия описывается количеством тепла. Это также может относиться к энтропии, когда тепло сравнивается с температурой. Режим описания нарушается для величин, проявляющих гистерезисные эффекты .
Вероятно, что термин «функции состояния» использовался в широком смысле в 1850-х и 60-х годах такими учёными, как Рудольф Клаузиус , Уильям Ранкин , Питер Тейт , Уильям Томсон , и широкое использование приобрёл к 1870-м годам. Например, в 1873 году Уиллард Гиббс в своей статье «Графические методы в термодинамике жидкостей» утверждает: "Величины V, B, T, U и S определяются, когда задано состояние тела, и их можно называть функциями состояния тела .
Рассмотрим две дефиниции термина «переменная состояния» , используемые в литературе по термодинамике. Согласно первой из них переменные состояния (параметры состояния, термодинамические параметры) представляют собой физические величины, характеризующие равновесное состояние термодинамической системы . Согласно второй дефиниции переменная состояния — физическая величина, характеризующая состояние термодинамической системы , одна из совокупности термодинамических величин, характеризующих состояние термодинамической системы и допускающая измерение с требуемой точностью .
Отличие в дефинициях (состояние и равновесное состояние) ведёт к тому, что область применения второй из дефиниций шире, нежели первой дефиниции, используемой в классической термодинамике равновесных состояний и процессов (классической равновесной термодинамике), вследствие чего в классической равновесной термодинамике глобальное (для системы в целом) описание неравновесных состояний и неравновесных процессов невозможно . Отсюда следует, что использование первой — более узкой — дефиниции переменной состояния исключает возможность обсуждения в классической равновесной термодинамике таких обычных для технической термодинамики вопросов, как рассмотрение стационарных неравновесных процессов в потоке и эксергетический анализ реальных неравновесных процессов .
Вторая дефиниция переменной состояния разрешает распространить это понятие на неравновесные состояния , то есть допускает рассмотрение методами классической термодинамики не только равновесных, но и неравновесных процессов путём замены условия равновесности изучаемой системы на требование её однородности , а взамен равновесных процессов рассматривают процессы квазистатические, что позволяет не учитывать в явном виде зависимость термодинамических величин от времени . Такой подход к логической системе построения/изложения термодинамики реализован в технической термодинамике, базирующейся не на классической равновесной термодинамике, а на классической термодинамике идеальных процессов . Согласно второй — более широкой — дефиниции переменной состояния глобальное состояние любой однородной термодинамической системы — как равновесной, так и неравновесной — характеризуют мгновенными значениями переменных состояния в каждый момент времени; для равновесной или стационарной неравновесной системы мгновенные значения переменных состояния постоянны и от времени не зависят. Кроме того, классическая термодинамика идеальных процессов использует представление о квазистатических процессах , по традиции именуемых обратимыми, призванных подменить рассмотрение реальных термодинамических процессов анализом их идеализированных моделей , в рамках поставленной задачи считающихся процессами бесконечно медленными (то есть длительность протекания квазистатического равновесного процесса должна намного превышать характерные времена релаксации системы ), что и позволяет для квазистатических процессов не учитывать в явном виде зависимость термодинамических величин от времени.
Важно, что вторая дефиниция переменной состояния, не упоминающая, что эта величина есть характеристика равновесной термодинамической системы, автоматически снимает необходимость обращения к принципу локального равновесия при построении термодинамики неравновесных процессов .
Термодинамическая система описывается рядом термодинамических параметров (например, температура , объём, давление ), которые не обязательно являются независимыми. Число параметров, необходимых для описания системы, является размерностью пространства состояний системы ( D ). Например, одноатомный газ , имеющий фиксированное число частиц, представляет собой простой случай двумерной системы ( D = 2 ). В этом примере любая система однозначно определяется двумя параметрами, такими как давление и объём или, возможно, давление и температура. Такой выбор параметров эквивалентен, поскольку он описывает разные системы координат в двумерном термодинамическом пространстве состояний. Из давления и температуры вычисляется объём. Точно так же, из давления и объёма вычисляется температура. Аналогичное утверждение справедливо для многомерных пространств, описываемых постулатом о термодинамическом состоянии.
Как правило, термодинамическая функция состояния имеет вид
где P — давление, T — температура, V — объём, а точки обозначают другие возможные термодинамические параметры, например N — число частиц и энтропию S . Если пространство состояния двумерно, как в примере выше, то пространство можно представить себе как поверхность в трёхмерном пространстве. Однако, обозначения для осей выбираются неоднозначным образом, поскольку есть более чем три термодинамических параметра.
Когда система непрерывно изменяет своё состояние, она отслеживает термодинамический «путь» в пространстве состояний. Путь можно указать, отметив значения параметров состояния, по мере изменения состояния, например, как функцию времени или какой-либо другой внешней переменной. Например, мы могли бы задать давление и объём как функции времени от и до момента ; это укажет путь в нашем примере в двумерном пространстве состояний. Теперь можно сформировать все возможные функций времени, которые можно проинтегрировать по пути. Например, если мы хотим рассчитать работу, выполненную системой между моментами времени и следует вычислить интеграл
Понятно, что для вычисления работы W в приведенном выше интеграле нам нужно знать функции и в каждый момент времени , в любой точке пути. Термодинамическая функция состояния — это функция параметров системы, которая зависит только от значений параметров в конечных точках пути. Например, предположим, что мы хотим рассчитать работу плюс интеграл от по выбранному пути. Тогда
Видно, что подынтегральное выражение можно выразить как точный дифференциал функции и, следовательно, интеграл выражается как разница значении в конечных точках интервала интегрирования. Поэтому произведение тоже является функцией состояния системы.
Используем d для обозначения полного дифференциала. Другими словами, интеграл будет равен . Символ δ будет зарезервирован для неточного дифференциала, который не может быть проинтегрирован без полного знания пути. Например, будет использоваться для обозначения бесконечно малого прироста работы.
Лучше всего рассматривать функции состояния как величины или свойства термодинамической системы, в то время как функции, не связанные с состоянием, представляют процесс, в ходе которого функции состояния изменяются. Например, функция состояния пропорционально внутренней энергии идеального газа, но — это количество энергии, передаваемой системой во время работы. Внутренняя энергия идентифицируется как особая форма энергии. Работа — это количество энергии, которая изменила свою форму или местоположение.
Следующие функции считаются функциями состояния в термодинамике :
|
|