Статья является частью одноименной серии.
Термодинамика
Уравнение состояния Термодинамические величины Термодинамические потенциалы Термодинамические циклы Фазовые переходы
См. также «Физический портал»

Идеа́льный газ — теоретическая модель , широко применяемая для описания свойств и поведения реальных газов при умеренных давлениях и температурах . В этой модели, во-первых, предполагается, что составляющие газ частицы не взаимодействуют друг с другом, то есть их размеры пренебрежимо малы, поэтому в объёме , занятом идеальным газом, нет взаимных неупругих столкновений частиц. Частицы идеального газа претерпевают столкновения только со стенками сосуда. Второе предположение: между частицами газа нет дальнодействующего взаимодействия, например, электростатического или гравитационного. Дополнительное условие упругих столкновений между молекулами и стенками сосуда в рамках молекулярно-кинетической теории приводит к термодинамике идеального газа .

В различных расширенных моделях идеального газа предполагается, что частицы имеют внутреннюю структуру и протяжённые размеры, что можно представить частицы в виде эллипсоидов или сфер, соединённых упругими связями (например, двухатомные молекулы). Представление частиц газа в виде многоатомных молекул приводит к возникновению дополнительных степеней свободы, что побуждает учитывать энергию не только поступательного, но и вращательно-колебательного движения частиц, а также не только центральные, но и нецентральные столкновения частиц .

Модель широко применяется для решения задач термодинамики газов и аэрогазодинамики . Например, воздух при атмосферном давлении и комнатной температуре с достаточной для практических расчётов точностью хорошо описывается моделью идеального газа.

В случае очень больших давлений требуется применение более точных уравнений состояния реальных газов, например, полуэмпирического уравнения Ван-дер-Ваальса , в котором учитывается притяжение между молекулами и их конечные размеры. При очень высоких температурах молекулы реальных газов могут диссоциировать на составляющие их атомы, или атомы могут ионизироваться с отщеплением электронов. Поэтому в случаях высоких давлений и/или температур уравнения состояния идеального газа применимы только с некоторыми допущениями, либо неприменимы совсем.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и подчиняются статистике Максвелла — Больцмана ) , квазиклассический идеальный газ (для которого — в отличие от классического идеального газа — не выполняется закон равномерного распределения энергии по степеням свободы ) и квантовый идеальный газ (его свойства определяются законами квантовой механики и описываются статистиками Ферми — Дирака или Бозе — Эйнштейна ) .

С термодинамической точки зрения различие между классическим и квазиклассическим идеальными газами состоит в следующем. Теплоёмкость классического идеального газа не зависит от температуры и однозначно задана геометрией молекулы газа , которая тем самым определяет вид калорического уравнения состояния газа. Классические идеальные газы с одинаковой геометрией молекул подчиняются одному и тому же калорическому уравнению состояния. Теплоёмкость квазиклассического идеального газа зависит от температуры , причём эта зависимость индивидуальна для каждого газа; соответственно каждый квазиклассический идеальный газ описывается своим собственным калорическим уравнением состояния. Очень часто — в том числе и в данной статье, — когда различия между классическим и квазиклассическим приближениями не играют роли, термин «классический идеальный газ» рассматривают как синоним выражения « неквантовый идеальный газ ». При макроскопическом подходе идеальными классическими и квазиклассическими газами называют гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона (Клапейрона — Менделеева ). Иногда дополнительно указывают, что для классического идеального газа справедлив закон Джоуля . Термодинамика утверждает, что закон Джоуля выполняется для любого флюида с уравнением состояния вида ${\displaystyle {\frac {p}{T}}=f(V)}$ или ${\displaystyle pV=f(T)}$ , где ${\displaystyle p}$ — давление , ${\displaystyle T}$ — абсолютная температура и ${\displaystyle V}$ — объём (см. ). Поэтому, давая дефиницию классическому идеальному газу, упоминать о законе Джоуля необязательно. С другой стороны, если рассматривать данный закон как обобщение экспериментальных данных, то изложение макроскопической теории классического идеального газа требует привлечения только самых элементарных сведений из термодинамики.

Популярность модели «идеальный газ» в учебных курсах термодинамики обусловлена тем обстоятельством, что результаты, получаемые с помощью уравнения Клапейрона, представляют собой не слишком сложные математические выражения и обычно допускают простой аналитический и/или графический анализ поведения входящих в них величин. Квазиклассическое приближение используют для вычисления термодинамических функций газов по их молекулярным данным .

История

История возникновения понятия идеальный газ восходит к успехам экспериментальной физики, начало которым было положено в XVII веке. В 1643 г. Эванджелиста Торричелли впервые доказал, что воздух имеет вес (массу), и, совместно с В. Вивиани , провёл опыт по измерению атмосферного давления с помощью запаянной с одного конца стеклянной трубки, заполненной ртутью. Так появился на свет первый ртутный барометр. В 1650 г. немецкий физик Отто фон Герике изобрёл воздушный насос и провёл в 1654 году знаменитый эксперимент с магдебургскими полушариями , наглядно подтвердивший существование атмосферного давления. Эксперименты английского физика Роберта Бойля по уравновешиванию ртутного столба давлением сжатого воздуха привели в 1662 году к выводу газового закона, названного впоследствии законом Бойля — Мариотта , в связи с тем, что французский физик Эдм Мариотт в 1679 г. провёл аналогичное независимое исследование.

В 1802 году французский физик Гей-Люссак опубликовал в открытой печати закон объёмов (называемый в русскоязычной литературе законом Гей-Люссака ) , однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году . Независимо от них этот закон был открыт в 1801 году английским физиком Джоном Дальтоном . Кроме того, качественно он был описан французским учёным Гийомом Амонтоном в конце XVII века. Гей-Люссак также установил, что коэффициент объёмного расширения одинаков для всех газов, несмотря на общепринятое мнение, что разные газы расширяются при нагревании различным образом.

Гей-Люссак (1822) и Сади Карно (1824) были первыми, кто объединил в едином уравнении законы Бойля — Мариотта и Шарля — Дальтона — Гей-Люссака. Поскольку, однако, Гей-Люссак найденным им уравнением не пользовался, а с полученными Карно результатами знакомились не по его ставшей библиографической редкостью книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу» , а по изложению идей Карно в работе Бенуа Клапейрона «Мемуар о движущей силе огня» , то и вывод термического уравнения состояния идеального газа приписали Клапейрону , а уравнение стали называть уравнением Клапейрона , хотя сам этот учёный никогда не претендовал на авторство обсуждаемого уравнения . Не вызывает, между тем, сомнения, что именно Клапейрон первый понял плодотворность применения уравнения состояния, существенно упрощавшего все связанные с газами расчёты.

Экспериментальные исследования физических свойств реальных газов в те годы были не вполне точны и проводились в условиях не сильно отличавшихся от нормальных (температура 0 ℃, давление 760 мм рт. ст. ). Предполагалось также, что газ, в отличие от пара , представляет собой субстанцию, неизменную в любых физических условиях. Первый удар по этим представлениям нанесло сжижение хлора в 1823 г. В дальнейшем выяснилось, что реальные газы представляют собой перегретые пары , достаточно удалённые от областей конденсации и критического состояния. Любой реальный газ может быть превращён в жидкость путём конденсации, либо путём непрерывных изменений однофазового состояния. Таким образом выяснилось, что реальные газы представляют одно из агрегатных состояний соответствующих простых тел, а точным уравнением состояния газа может быть уравнение состояния простого тела. Несмотря на это, газовые законы сохранились в термодинамике и в её технических приложениях как законы идеальных газов — предельных (практически недостижимых) состояний реальных газов . Уравнение Клапейрона было выведено при некоторых допущениях на основе молекулярно-кинетической теории газов ( Августом Крёнигом в 1856 г. и Рудольфом Клаузиусом в 1857 г.) . Клаузиусом было введено и само понятие «идеальный газ» (в отечественной литературе конца XIX — начала XX веков вместо названия «идеальный газ» использовали термин «совершенный газ» ).

Следующий важный шаг в формулировке термического уравнения состояния идеального газа — переход от индивидуальной для каждого газа постоянной к универсальной газовой постоянной — сделал русский инженер Илья Алымов , работа которого, опубликованная в малоизвестном среди физиков и химиков издании, не обратила на себя внимание. Этот же результат был получен Менделеевым в 1874 году . Независимо от работ русских учёных (1866) , Като Гульдберг (1867) и (1873) пришли к выводу, что произведение индивидуальной для каждого газа постоянной в уравнении Клапейрона на молекулярный вес газа должно быть постоянной для всех газов величиной.

В 1912 году при выводе постоянной Нернста был впервые применён принцип разделения фазового пространства на равновеликие ячейки. Впоследствии в 1925 году Ш. Бозе опубликовал статью «Закон Планка и гипотеза о световых квантах», в которой развил эту идею применительно к фотонному газу. Эйнштейн сказал о данной статье, что «использованный здесь метод позволяет получить квантовую теорию идеального газа» . В декабре того же года Энрико Ферми разработал статистику частиц с полуцелым спином , подчиняющихся принципу Паули , которые позднее назвали фермионами .

В отечественной литературе, изданной до конца 1940-х годов, термическое уравнение состояния идеального газа называли уравнением Клапейрона или уравнением Клапейрона для 1 моля . В фундаментальной отечественной монографии 1948 года, посвящённой различным уравнениям состояния газов , Менделеев — в отличие от Клапейрона — вообще не упоминается. Фамилия Менделеева в названии рассматриваемого нами уравнения появилась после начала «борьбы с низкопоклонством перед Западом» и поиска «русских приоритетов» . Тогда-то и стали в научной и учебной литературе использовать такие варианты названия, как уравнение Менделеева , уравнение Менделеева — Клапейрона и уравнение Клапейрона — Менделеева .

Классический идеальный газ

Молекулярно-кинетическая теория идеального газа

Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

• Размеры молекул пренебрежимо малы по сравнению со средним расстоянием между ними, так что суммарный объём, занимаемый молекулами, много меньше объёма сосуда ;
• импульс передаётся только при соударениях, то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях ;
• соударения частиц между собой и со стенками сосуда абсолютно упруги ;
• количество молекул в газе велико и фиксированно, что позволяет вычислять средние величины по малому (по сравнению с размерами системы) объёму;
• газ находится в термодинамическом равновесии со стенками сосуда и дополнительно отсутствуют макроскопические потоки вещества. Тут следует уточнить, что градиенты термодинамических величин могут иметь место, как например при включении внешнего поля, к примеру гравитационного.

В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно полному импульсу, передаваемому при столкновении частиц с участком стенки единичной площади в единицу времени , внутренняя энергия — сумме энергий частиц газа .

По эквивалентной макроскопической формулировке идеальный газ — такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака , то есть:

${\displaystyle pV=\mathrm {const} \cdot T,}$

где ${\displaystyle p}$ — давление, ${\displaystyle V}$ — объём, ${\displaystyle T}$ — абсолютная температура.

Термическое уравнение состояния и термические коэффициенты идеального газа

Термические свойства классического и квазиклассического идеального газа описываются уравнением Клапейрона :

${\displaystyle pV={\frac {m}{M}}RT\,,}$

где R — универсальная газовая постоянная (8,3144598 Дж ⁄ ( моль ∙К) ), m — масса газа, M — его молярная масса , или

${\displaystyle pV=\nu RT}$ ,

где ${\displaystyle \nu }$ — количество газа в молях .

В формулах статистической физики принято использовать постоянную Больцмана k (1,3806·10 ⁻²³ Дж ⁄ К ) , массу частицы ${\displaystyle {\acute {m}}}$ и число частиц N .

Статистические и термодинамически величины связаны соотношениями:

${\displaystyle m={\acute {m}}N,~~~n={\frac {N}{N_{A}}},~~~R=kN_{A},~~~kN=nR\,,}$

где N _А — число Авогадро (6,02214·10 ²³ 1 ⁄ моль ).

С использованием обозначений статистической физики уравнение Клапейрона принимает вид:

${\displaystyle pV=NkT\,,}$

или:

${\displaystyle p=ckT\,,}$

где c — концентрация частиц .

Сведения, касающиеся термических коэффициентов идеального газа, изложены в статье Уравнение состояния .

Смесь идеальных газов

Смесь идеальных газов тоже идеальный газ. Каждой компоненте газа соответствует своё парциальное давление и общее давление смеси есть сумма парциальных давлений компонент смеси ${\displaystyle p=p_{1}+p_{2}+p_{3}}$ … Также можно получить общее количество молей в смеси газов как сумму ${\displaystyle n=n_{1}+n_{2}+n_{3}}$ … Тогда уравнение состояния для смеси идеальных газов

${\displaystyle pV=nRT\,.}$

Совершенный газ (гидроаэромеханика)

В отличие от термодинамики в гидроаэромеханике газ, подчиняющийся уравнению Клапейрона, называют совершенным . У совершенного газа молярные изохорная ${\displaystyle C_{V}}$ и изобарная ${\displaystyle C_{P}}$ теплоёмкости постоянны. В то же время идеальным в гидроаэромеханике называют газ, у которого отсутствуют вязкость и теплопроводность . Модель совершенного газа широко применяют при исследовании течения газов .

Теплоёмкость

Определим теплоёмкость при постоянном объёме для идеального газа как

${\displaystyle {\hat {c}}_{V}={\frac {1}{nR}}T\left({\frac {\partial S}{\partial T}}\right)_{V}={\frac {1}{nR}}\left({\frac {\partial U}{\partial T}}\right)_{V}\,,}$

где S — энтропия . Это безразмерная теплоёмкость при постоянном объёме, которая обычно зависит от температуры из-за межмолекулярных сил. При умеренных температурах это константа: для одноатомного газа ĉ _V = 3/2, для двухатомного газа и многоатомных газов с линейными молекулами это ĉ _V = 5/2, а для многоатомного газа с нелинейными молекулами ĉ _V = 6/2=3. Видно, что макроскопические измерения теплоёмкости могут дать информацию о микроскопической структуре молекул. В отечественной учебной литературе, где понятие безразмерной теплоёмкости не получило распространения, для классического идеального газа его теплоёмкость при постоянном объёме C _V полагают не зависящей от температуры и, согласно теореме о равнораспределении , равной : 3 Rν /2 для всех одноатомных газов, 5 Rν /2 для всех двухатомных газов и многоатомных газов с линейными молекулами, 3 Rν для всех многоатомных газов с нелинейными молекулами. Отличие квазиклассического идеального газа от классического состоит в ином виде зависимости внутренней энергии газа от его температуры . Для классического идеального газа его теплоёмкость при постоянном объёме C _V не зависит от температуры (она составляет), то есть внутренняя энергия газа всегда пропорциональна его температуре; для квазиклассического идеального газа его теплоёмкость ${\displaystyle C_{V}}$ зависит от химического состава газа и температуры, то есть имеет место нелинейная зависимость внутренней энергии газа от температуры .

Теплоёмкость при постоянном давлении 1/R моль идеального газа:

${\displaystyle {\hat {c}}_{P}={\frac {1}{nR}}T\left({\frac {\partial S}{\partial T}}\right)_{P}={\frac {1}{nR}}\left({\frac {\partial H}{\partial T}}\right)_{P}={\hat {c}}_{V}+1\,,}$

где H = U + PV — энтальпия газа.

Иногда проводится различие между классическим идеальным газом, где ĉ _V и ĉ _P могут меняться с температурой и квазиклассическим идеальным газом, для которого это не так.

Для любого классического и квазиклассического идеального газа справедливо соотношение Майера :

${\displaystyle C_{P}-C_{V}=R\,,}$

где ${\displaystyle C_{P}}$ — молярная теплоёмкость при постоянном давлении.

Соотношение теплоёмкостей при постоянном объёме и постоянном давлении

${\displaystyle \gamma ={\frac {c_{P}}{c_{V}}}}$

называется показателем адиабаты . Для воздуха, представляющего собой смесь газов, это соотношение составляет 1,4. Для показателя адиабаты справедлива теорема Реша :

${\displaystyle {\frac {C_{P}}{C_{V}}}={\frac {\left({\frac {\partial P}{\partial V}}\right)_{S}}{\left({\frac {\partial P}{\partial V}}\right)_{T}}}\,.}$

(Теорема Реша)

Энтропия и термодинамические потенциалы

Выражая C _V в терминах ĉ _V как было показано в предыдущем разделе, дифференцируя уравнение состояния идеального газа и интегрируя можно получить выражение энтропии :

${\displaystyle \Delta S={\hat {c}}_{V}Nk\ln \left({\frac {T}{T_{0}}}\right)+Nk\ln \left({\frac {V}{V_{0}}}\right)\,,}$

Данное выражение, после ряда преобразований позволяет получить термодинамические потенциалы для идеального газа как функции T , V , и N в виде :

${\displaystyle U\,}$		${\displaystyle ={\hat {c}}_{V}NkT\,}$
${\displaystyle A\,}$	${\displaystyle =U-TS\,}$	${\displaystyle =\mu N-NkT\,}$
${\displaystyle H\,}$	${\displaystyle =U+PV\,}$	${\displaystyle ={\hat {c}}_{P}NkT\,}$
${\displaystyle G\,}$	${\displaystyle =U+PV-TS\,}$	${\displaystyle =\mu N\,,}$

где, как и раньше,

${\displaystyle {\hat {c}}_{P}={\hat {c}}_{V}+1\,.}$

Применение теории идеального газа

Физический смысл температуры газа

В рамках молекулярно-кинетической теории давление молекул газа на стенку сосуда ${\displaystyle p={\frac {F}{S}}}$ равно отношению силы ${\displaystyle F}$ , действующей на стенку со стороны молекул, к площади стенки ${\displaystyle S}$ . Силу можно вычислить как отношение суммарного импульса ${\displaystyle K}$ , переданного стенке при столкновениях молекул за время ${\displaystyle \Delta t}$ , к длительности этого интервала:

${\displaystyle p={\frac {K}{S\Delta t}}.\qquad \qquad }$

При упругом соударении молекула массы ${\displaystyle m}$ передаёт стенке импульс

${\displaystyle k_{m}=2mv\cos \vartheta ,\qquad \qquad }$

где ${\displaystyle \vartheta }$ — угол между импульсом молекулы до соударения и нормалью со стенкой и ${\displaystyle v}$ — скорость молекулы . Число соударений со стенкой равно ${\displaystyle N_{\rm {st}}=nvS\cos \vartheta \Delta t.}$ Усреднение выражения ${\displaystyle K=k_{m}N_{\rm {st}}}$ по всем возможным углам и скоростям, даёт:

${\displaystyle K={\frac {2}{3}}n\varepsilon _{\rm {kin}}S\Delta t,\qquad \qquad }$ ,

где ${\displaystyle \ \varepsilon _{\rm {kin}}}$ — средняя кинетическая энергия поступательного движения молекул газа. Подставив это выражение ${\displaystyle K}$ в формулу для ${\displaystyle p}$ , получаем, что давление молекул на стенку сосуда определяется как ${\displaystyle p={\frac {2}{3}}n\varepsilon _{\rm {kin}}}$ , Подставив ${\displaystyle p}$ в уравнение Клапейрона в форме ${\displaystyle p=nkT}$ , имеем выражение ${\displaystyle \ \varepsilon _{\rm {kin}}={\frac {3}{2}}kT}$ , откуда следует, что температура газа прямо пропорциональна средней энергии поступательного движения молекул .

Распределение Больцмана

Равновесное распределение частиц классического идеального газа по состояниям можно получить следующим образом. Используя выражение для потенциальной энергии газа в гравитационном поле и уравнение Клапейрона, выводят барометрическую формулу и с её помощью находят распределение молекул газа по энергиям в гравитационном поле. Больцман показал, что полученное таким образом распределение справедливо не только в случае потенциального поля сил земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения . Это распределение и носит название распределения Больцмана :

${\displaystyle {\bar {n}}_{j}=ae^{-{{\varepsilon _{j}} \over {kT}}}\,,}$

где ${\displaystyle {\bar {n}}_{j}}$ — среднее число частиц, находящихся в ${\displaystyle j}$ -ом состоянии с энергией ${\displaystyle \varepsilon _{j}}$ , а константа ${\displaystyle a}$ определяется условием нормировки:

${\displaystyle \sum {n_{j}}=N\,,}$

где ${\displaystyle N}$ — полное число частиц.

Распределение Больцмана является предельным случаем распределений Ферми — Дирака и Бозе — Эйнштейна для больших температур, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа . Данный предельный случай соответствует ситуации, когда заполнение энергетических уровней невелико и квантовыми эффектами можно пренебречь .

Адиабатический процесс

C помощью модели идеального газа можно предсказать изменение параметров состояния газа при адиабатическом процессе. Запишем уравнение Клапейрона в таком виде:

${\displaystyle pV=\nu RT\,.}$

Продифференцировав обе части, получаем:

${\displaystyle pdV+Vdp=\nu RdT}$ .

Согласно экспериментально установленному закону Джоуля (закону Гей-Люссака — Джоуля) внутренняя энергия идеального газа не зависит от давления или объёма газа . По определению молярной теплоёмкости при постоянном объёме, ${\displaystyle \left({\frac {\partial U}{\partial T}}\right)_{V}=C_{V}}$ . Поэтому получаем

${\displaystyle \mathrm {d} U=\nu C_{V}\mathrm {d} T\,,}$

где ${\displaystyle \nu }$ — число молей идеального газа.

Учитывая отсутствие теплообмена с окружающей средой имеем :

${\displaystyle \mathrm {d} U=-p\,\mathrm {d} V.}$

C учётом этого уравнение Клапейрона приобретает вид

${\displaystyle p\mathrm {d} V+V\mathrm {d} p=-p\mathrm {d} V\cdot {\frac {R}{C_{V}}}\,,}$

далее, введя коэффициент ${\displaystyle {\mathsf {\gamma }}=1+R/C_{V}}$ , получаем окончательно уравнение Пуассона :

${\displaystyle p\,\cdot V^{\mathsf {\gamma }}=\mathrm {const} \,.}$

Для нерелятивистского невырожденного одноатомного идеального газа ${\displaystyle \gamma =5/3}$ , двухатомного ${\displaystyle \gamma =7/5}$ .

Скорость звука

Скорость звука в идеальном газе определяется

${\displaystyle c_{s}={\sqrt {\left({\frac {\partial P}{\partial \rho }}\right)_{s}}}={\sqrt {\frac {\gamma P}{\rho }}}={\sqrt {\frac {\gamma RT}{M}}}\,,}$

где γ — показатель адиабаты ( ĉ _P /ĉ _V ), s — энтропия на частицу газа, ρ — плотность газа, P — давление газа, R — универсальная газовая постоянная , T — температура , M — молярная масса газа. Так как колебания плотности быстрые, то процесс в целом происходит без обмена теплом, что объясняет появление показателя адиабаты в выражении для скорости звука. Для воздуха возьмём γ = 1,4, M =28,8, T = 273 К, тогда c _s =330 м/с.

Квантовый идеальный газ

Понижение температуры и увеличение плотности газа может привести к ситуации, когда среднее расстояние между частицами становится соизмеримым с длиной волны де Бройля для этих частиц, что приводит к переходу от классического к квантовому идеальному газу. В таком случае поведение газа зависит от спина частиц: в случае полуцелого спина ( фермионы ) действует статистика Ферми — Дирака ( Ферми-газ ), в случае целого спина ( бозоны ) — статистика Бозе — Эйнштейна ( Бозе-газ ) .

Ферми-газ

Для фермионов действует принцип Паули , запрещающий двум тождественным фермионам находиться в одном квантовом состоянии . Вследствие этого при абсолютном нуле температуры импульсы частиц и, соответственно, давление и плотность энергии Ферми-газа отличны от нуля и пропорциональны числу частиц в единице объёма . Существует верхний предел энергии, который могут иметь частицы Ферми-газа при абсолютном нуле ( Энергия Ферми ${\displaystyle E_{F}}$ ). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом .

Примерами Ферми-газов являются электронный газ в металлах , сильнолегированных и вырожденных полупроводниках , вырожденный газ электронов в белых карликах .

Бозе-газ

Так как бозоны могут быть строго тождественны друг другу и, соответственно, принцип Паули на них не распространяется, то при снижении температуры Бозе-газа ниже некоторой температуры ${\displaystyle T_{0}}$ возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе — Эйнштейна . Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при ${\displaystyle T<T_{0}}$ давление Бозе-газа зависит только от температуры. Этот эффект в 1995 году наблюдался экспериментально, а в 2001 году авторам эксперимента была присуждена Нобелевская премия .

Примерами Бозе-газов являются различного рода газы квазичастиц (слабых возбуждений) в твёрдых телах и жидкостях , сверхтекучая компонента гелия II, конденсата Бозе — Эйнштейна куперовских электронных пар при сверхпроводимости . Примером ультрарелятивистского бозе-газа является фотонный газ ( тепловое излучение ) . Примером бозе-газа, состоящего из квазичастиц является фононный газ .

Идеальный газ в гравитационном поле

В ОТО-релятивистской термодинамике при термическом равновесии газовой (жидкой) сферы собственная температура, измеряемая местным наблюдателем, понижается при перемещении по радиусу от центра сферы к её поверхности. Этот релятивистский эффект невелик (исключая случай сверхсильных гравитационных полей) и у поверхности Земли им пренебрегают .

Реальное воздействие гравитационного поля на газ (жидкость) проявляется в первую очередь через зависимость гидростатического давления от высоты столба газа (жидкости). Влияние поля тяготения на термодинамические свойства системы можно не учитывать в том случае, когда изменение давления по высоте много меньше абсолютной величины давления. Не выходя за рамки термодинамики, Дж. Максвелл установил , что «…в вертикальной колонне газа, предоставленного самому себе, температура повсюду одинакова после того, как колонна достигла теплового равновесия посредством теплопроводности; другими словами, тяжесть не оказывает никакого влияния на распределение температур в колонне», и что этот вывод справедлив для любых газов (жидкостей), то есть равенство температур по всему объёму системы есть необходимое условие равновесия в гравитационном поле . Методами молекулярно-кинетической теории этот же результат для газов был получен Л. Больцманом .

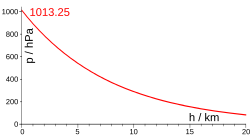
Зависимость давления от высоты изотермического столба идеального газа даёт барометрическая формула . В простейшей термодинамической модели, объясняющей наблюдаемую неизотермичность земной атмосферы , рассматривают не равновесное , а стационарное состояние столба идеального газа, достигаемое равновесным адиабатическим процессом циркуляции воздуха , когда теплопередача в сторону убыли температуры (вверх), уравновешивается переносом потенциальной энергии молекул воздуха в обратном направлении .

Пределы применимости теории идеального газа

Если плотность газа повышается, то столкновения молекул начинают играть всё бо́льшую роль и пренебрегать размерами и взаимодействием молекул становится невозможным. Поведение такого газа плохо описывается моделью идеального газа, в связи с чем его называют реальным газом . Аналогично моделью идеального газа нельзя пользоваться при описании плазмы, в которой присутствует значительное взаимодействие между отдельными молекулами . Для описания реальных газов применяются различные модифицированные уравнения состояния, например, вириальное разложение .

Другое широко используемое уравнение получается, если учесть, что молекула не бесконечно мала, а имеет определённый диаметр ${\displaystyle d}$ , то уравнение Клапейрона для одного моля газа примет вид :

${\displaystyle p(V-b)=RT\,,}$

при этом величина ${\displaystyle b}$ равна :

${\displaystyle b={\frac {2\pi }{3}}Nd^{3}\,,}$

где ${\displaystyle N}$ — число молекул в газе. Учёт дополнительно сил межмолекулярного притяжения ( сил Ван-дер-Ваальса ) приведёт к изменению уравнения до уравнения Ван-дер-Ваальса :

${\displaystyle \left(p+{\frac {a\nu ^{2}}{V^{2}}}\right)\left({V}-{b\nu }\right)=\nu RT\,.}$

Существует ряд эмпирических уравнений состояния, например Бертло и , которые ещё лучше описывают поведение реального газа в определённых условиях .

Примечания

Комментарии

Источники

Литература