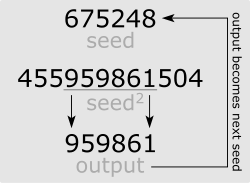
В математике и информатике метод средних квадратов — это метод генерации псевдослучайных чисел . Метод имеет непоправимые недостатки для многих практических применений, так как его период обычно очень короткий, а также: после некоторого количества итераций либо начнётся повторное генерирование одного и того же числа, либо последовательность зациклится на предыдущем числе.

История

Метод был изобретен Джоном фон Нейманом и изложен им на конференции в 1949 году.

В 1949 году фон Нейман заметил: «Любой, кто рассматривает арифметические методы получения случайных цифр, конечно, находится в состоянии греха». Он уточнил, что имел в виду, что не было никаких истинных «случайных чисел», а «строгая арифметическая процедура», как и метод средних квадратов, «не является таким методом». Тем не менее, он обнаружил, что эти методы в сотни раз быстрее, чем чтение «истинных» случайных чисел с перфокарт, что имело практическое значение для его работы. Он обнаружил, что «уничтожение» последовательностей средних квадратов является фактором в их пользу, потому что его можно легко обнаружить: «всегда боишься появления необнаруженных коротких циклов». Николас Метрополис сообщил о последовательности 750 000 цифр перед «уничтожением» с помощью 38-битных чисел с методом среднего квадрата.

Книга Ивара Экеланда «The Broken Dice» дает расширенное описание того, как метод был изобретен францисканским монахом, известным только как брат Эдвин, где-то между 1240 и 1250 годами. Предположительно, рукопись теперь потеряна, но Хорхе Луис Борхес отправил Экеланду копию, которую он сделал в Ватиканской библиотеке.

Изменение алгоритма среднего квадрата с помощью _en улучшает период и случайность.

Метод

Для генерации последовательности n-значных псевдослучайных чисел создаётся n-значное начальное значение, образующее 2n-значное число. Если результат имеет менее 2n цифр, для компенсации добавляются ведущие нули. Средние n цифр результата будут следующим числом в последовательности и будут возвращены в результате. Затем этот процесс повторяется для получения большего количества чисел.

Значение n должно быть четным, чтобы метод работал — если значение n нечётное, то не обязательно будет существовать единственно определенная «середина из n цифр» для выбора. Рассмотрим следующее: если трехзначное число возвести в квадрат, то может получиться шестизначное число (например, 540 ² = 291600). Если бы существовала середина из 3 цифр, то осталось бы 6 − 3 = 3 цифры, которые нужно было бы распределить слева и справа от середины. Невозможно равномерно распределить эти цифры симметрично по обе стороны от середины числа, поэтому «серединных цифр» нет. Допустимо дополнять исходные значения нулями слева, чтобы получить число с чётным значением n (например, 540 → 0540).

Для генератора n -значных чисел период может быть не более 8n . Если середина числа состоит только из нулей, то генератор будет бесконечно выводить нули. Если первая половина числа в последовательности состоит из нулей, последующие числа будут убывать до нуля. И хотя эти серии из нулей легко обнаружить, они возникают слишком часто, чтобы этот метод был практически полезным. Метод среднего квадрата также может застрять на числе, отличном от нуля. Для n = 4 это происходит с значениями 0100, 2500, 3792 и 7600. Другие начальные значения образуют очень короткие повторяющиеся циклы, например, 0540 → 2916 → 5030 → 3009. Эти явления становятся еще более очевидными, когда n = 2, так как ни одно из 100 возможных исходных значений не генерирует более 14 итераций без возврата к 0, 10, 50, 60 или циклу 24 ↔ 57.

Пример реализации

Программа на языке Python 3 :

seed_number = int(input("Введите число из 4 цифр:\n[####] "))
number = seed_number
already_seen = set()
counter = 0

while number not in already_seen:
    counter += 1
    already_seen.add(number)
    number = int(str(number * number).zfill(8)[2:6])
    print(f"#{counter}: {number}")

print(f"Мы начали с числа {seed_number} и"
      f" повторились через {counter} шагов"
      f" с числом {number}.")

Примечания