Оптимизация запросов СУБД
- 1 year ago
- 0
- 0
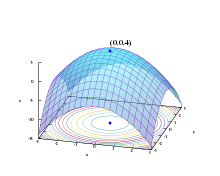
Оптимизация (в математике , информатике и исследовании операций ) — это задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства , ограниченной набором линейных и/или нелинейных равенств и/или неравенств .

Теорию и методы решения задачи оптимизации изучает математическое программирование .
Математическое программирование — это раздел математики , разрабатывающий теорию, численные методы решения многомерных задач оптимизации с ограничениями.
В процессе проектирования ставится обычно задача определения наилучшей, в некотором смысле, структуры или наилучших значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией . Задача выбора оптимальной структуры является структурной оптимизацией .
Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ * , который доставляет минимальное значение f(χ * ) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации, необходимо задать:
Тогда решить задачу означает одно из:
Если минимизируемая функция не является выпуклой , то часто ограничиваются поиском локальных минимумов и максимумов: точек таких, что всюду в некоторой их окрестности для минимума и для максимума.
Если допустимое множество , то такая задача называется задачей безусловной оптимизации , в противном случае — задачей условной оптимизации .
Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом).
Методы оптимизации классифицируют в соответствии с задачами оптимизации:
Существующие в настоящее время методы поиска можно разбить на три большие группы:
По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации .
По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:
По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:
Помимо того, оптимизационные методы делятся на следующие группы:
В зависимости от природы множества X задачи математического программирования классифицируются как:
Кроме того, разделами математического программирования являются параметрическое программирование , динамическое программирование и стохастическое программирование .
Математическое программирование используется при решении оптимизационных задач исследования операций .
Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:
Задачи линейного программирования были первыми подробно изученными задачами поиска экстремума функций при наличии типа неравенств . В 1820 году Фурье и затем в 1947 году Джордж Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод , ставший основным при решении задач линейного программирования.
Присутствие в названии дисциплины термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование , составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин « линейное программирование » был предложен Дж. Данцигом в 1949 году для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях.
Поэтому наименование «математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.
Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 1930-м годам. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман — математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель , носящую его имя, и Л. В. Канторович — советский академик, лауреат Нобелевской премии (1975), сформулировавший ряд задач линейного программирования и предложивший в 1939 году метод их решения ( ), незначительно отличающийся от симплекс-метода.
В 1931 году венгерский математик рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название « венгерского метода ».
Л. В. Канторович и М. К. Гавурин в 1949 году разработали метод потенциалов , который применяется при решении транспортных задач . В последующих работах Л. В. Канторовича, В. С. Немчинова , В. В. Новожилова , А. Л. Лурье , А. Брудно , А. Г. Аганбегяна , Д. Б. Юдина , Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования , так и приложение её методов к исследованию различных экономических проблем.
Методам линейного программирования посвящено много работ зарубежных учёных. В 1941 году поставил транспортную задачу . Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 году Дж. Данцигом. Дальнейшее развитие методы линейного и нелинейного программирования получили в работах Г. Куна , А. Таккера , Гасса (Saul I. Gass), Чарнеса (A. Charnes), (E. M. Beale) и др.
Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования , в которых либо целевая функция , либо ограничения, либо то и другое нелинейны. В 1951 году была опубликована работа Г. Куна и А. Таккера , в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.
Начиная с 1955 года опубликовано много работ, посвященных (работы Била, и Р. Дорфмана , (M. Frank) и , Г. Марковица и др.). В работах Денниса (J. B. Dennis), Розена (J. B. Rosen) и Зонтендейка (G. Zontendijk) разработаны градиентные методы решения задач нелинейного программирования.
В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны , представителями которыми являются AMPL и .