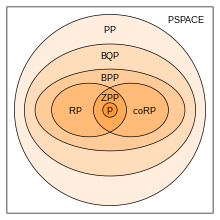
В теории вычислительной сложности ZPP ( англ. zero-error probabilistic polynomial time — безошибочный вероятностный полиномиальный ) — это класс задач с ответом «Да» либо «Нет», для которых существует вероятностная машина Тьюринга , удовлетворяющая следующим свойствам:

• Она всегда правильно отвечает «Да» либо «Нет».
• Математическое ожидание времени работы данной машины Тьюринга полиномиально (само время работы может быть неограниченно велико).

Существует альтернативный набор свойств:

• Машина Тьюринга всегда работает за полиномиальное время.
• Она отвечает «Да», «Нет» или «Не знаю».
• Ответ может быть либо правильным, либо «Не знаю».
• Если правильный ответ «Да», машина Тьюринга отвечает «Да» с вероятностью не меньше ½.
• Если правильный ответ «Нет», машина Тьюринга отвечает «Нет» с вероятностью не меньше ½.

Выбор одного из двух наборов свойств приводит к эквивалентным определениям класса ZPP. Машину Тьюринга, удовлетворяющую этим свойствам, иногда называют машиной Тьюринга типа Лас-Вегас .

Эквивалентное определение через пересечение

Класс ZPP равен пересечению классов RP и Co-RP . Часто именно это принимается за определение ZPP . Чтобы продемонстрировать это, заметим, что любая задача принадлежащая одновременно RP и co-RP имеет алгоритм типа Лас-Вегас :

• Допустим, существует язык L, распознаваемый RP -алгоритмом A и (возможно отличным от A ) co-RP -алгоритмом B .
• Выполним один шаг алгоритма A на входной последовательности. Если будет возвращен ответ «Да», то окончательный ответ должен быть «Да». В противном случае запустим один шаг алгоритма B с тем же входом. Если он ответит «Нет», то окончательный ответ должен быть «Нет». Если не выполнено ни одно из предыдущих условий, повторим данный шаг.

Заметим, что лишь один из алгоритмов A или B может дать неправильный ответ, и вероятность этого события равняется на каждом шаге 50 %. Таким образом, вероятность достигнуть k -го шага уменьшается экспоненциально относительно k . Это показывает, что математическое ожидание времени работы полиномиально. Из сказанного следует, что пересечение классов RP и co-RP содержится в ZPP .

Покажем, что ZPP содержится в пересечении RP и co-RP . Пусть имеется машина Тьюринга типа Лас-Вегас C , которая решает задачу. Обозначим математическое ожидание времени её работы за M (по условию, оно конечно). Тогда можно построить следующий RP алгоритм:

• Запустим C на время, не меньшее 2M . Если за это время C получила ответ — возвращаем его. Если до момента останова никакого ответа не получено, говорим «Нет».

Вероятность того, что ответ будет получен до момента останова, равняется ½ (из неравенства Маркова ). Это в свою очередь означает, что вероятность ответа «Нет» при правильном ответе «Да» (такое могло случиться из-за преждевременной остановки C ), равна ½, что удовлетворяет определению RP . Для доказательства включения ZPP в co-RP можно либо воспользоваться тем же рассуждением, либо заметить, что ZPP замкнут относительно взятия дополнения.

Литература

• J. Gill. (англ.) // Proceedings of the sixth annual ACM symposium on Theory of computing (STOC '74). — New York, NY, USA: Association for Computing Machinery, 1974. — P. 91–95 . — doi : .