Interested Article - Диэлектрическая проницаемость

- 2020-01-25
- 1
Диэлектри́ческая проница́емость ( и ) — коэффициент, входящий в математическую запись закона Кулона для силы взаимодействия точечных зарядов и , находящихся в однородной изолирующей (диэлектрической) среде на расстоянии друг от друга:
а также в уравнение связи вектора электрической индукции с напряжённостью электрического поля :
в рассматриваемой среде .
Вводятся абсолютная ( ) и относительная ( r, от лат. relativus [-a, -um] — относительный) проницаемости:
где — электрическая постоянная .
Cам термин «диэлектрическая проницаемость» применяется и для , и для ; ради краткости, одну из этих величин (в российской литературе чаще , в англоязычной ) переобозначают как (из контекста обычно ясно, о какой проницаемости идёт речь).
Величина безразмерна, а по размерности совпадает с (в Международной системе единиц (СИ): фарад на метр, Ф/м).
Проницаемость показывает, во сколько раз сила взаимодействия двух электрических зарядов в конкретной среде меньше, чем в вакууме , для которого .
Отличие проницаемости от единицы обусловлено эффектом поляризации диэлектрика под действием внешнего электрического поля , в результате которой создаётся внутреннее противоположно направленное поле. В области низких частот значение проницаемости реальных сред , обычно оно лежит в диапазоне 1—100, но для сегнетоэлектриков составляет десятки и сотни тысяч. Как функция частоты электрического поля величина слегка возрастает на участках вне полос или линий поглощения электромагнитного излучения данным материалом, однако вблизи линий или полос резко спадает, из-за чего высокочастотная диэлектрическая проницаемость ниже статической. Имеет место связь проницаемости и показателя преломления вещества: для немагнитной непоглощающей среды
Относительная диэлектрическая проницаемость является одним из «электромагнитных параметров» среды, влияющих на распределение компонент вектора напряжённости электромагнитного поля в пространстве и описывающих среду в материальных уравнениях электродинамики ( уравнениях Максвелла ).
Абсолютная диэлектрическая проницаемость вакуума
Электрическая постоянная , она же «абсолютная диэлектрическая проницаемость вакуума», в системе единиц СИ равна:
- Ф/м
(имеет размерность L −3 M −1 T 4 I 2 ).
В системе СГС эта же постоянная составляет однако часто в СГС вообще не используют , надлежащим образом видоизменяя формулы. Например, закон Кулона:
Электрическая постоянная связана с магнитной постоянной и скоростью света в вакууме:
Ниже все формулы приводятся для СИ, а символ используется как замена ( ).
Эффект поляризации диэлектрика и проницаемость
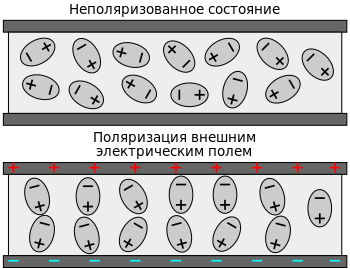
Под воздействием электрического поля в диэлектрике происходит поляризация — явление, связанное с ограниченным смещением зарядов относительно положения равновесия без наложенного электрического поля или поворотом электрических диполей .
Это явление характеризует вектор электрической поляризации равный дипольному моменту единицы объёма диэлектрика. В отсутствие внешнего поля диполи ориентированы хаотично (см. на рисунке сверху), за исключением особых случаев спонтанной поляризации в сегнетоэлектриках. При наличии поля диполи в большей или меньшей степени поворачиваются (на рисунке снизу), в зависимости от восприимчивости конкретного материала, а восприимчивость, в свою очередь, определяет проницаемость .
Помимо дипольно-ориентационного, имеются и другие механизмы поляризации. Поляризация не изменяет суммарного заряда в любом макроскопическом объёме однородного материала, однако она сопровождается появлением связанных электрических зарядов на поверхности диэлектрика и в местах неоднородностей среды. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле, как правило, направленное против внешнего наложенного поля. В итоге то, что является следствием электрической поляризации материалов.
Роль диэлектрической проницаемости среды в физике
Относительная диэлектрическая проницаемость среды, наряду с её относительной магнитной проницаемостью и удельной электропроводностью влияет на распределение напряжённости электромагнитного поля в пространстве и используется при описании среды в системе уравнений Максвелла .
Среду со значениями и называют идеальным диэлектриком (диэлектриком без поглощения, диэлектриком без потерь), для неё определяет такие вторичные параметры, как коэффициент преломления среды, скорость распространения, фазовую скорость и коэффициент укорочения длины электромагнитной волны в среде, волновое сопротивление среды.
Относительная диэлектрическая проницаемость реальных диэлектриков (диэлектриков с потерями, диэлектриков с поглощением, для которых ) также влияет на значение тангенса угла диэлектрических потерь и коэффициент поглощения электромагнитной волны в среде.
Относительная диэлектрическая проницаемость среды влияет на электрическую ёмкость расположенных в ней проводников : увеличение приводит к увеличению ёмкости. При изменении в пространстве (то есть, если зависит от координат) говорят о неоднородной среде , зависимость от частоты электромагнитных колебаний — одна из возможных причин дисперсии электромагнитных волн, зависимость от напряженности электрического поля — одна из возможных причин нелинейности среды . Если среда является анизотропной , то в материальном уравнении будет не скаляром, а тензором . При использовании метода комплексных амплитуд в решении системы уравнений Максвелла и наличии потерь в среде ( ) оперируют комплексной диэлектрической проницаемостью .
Таким образом, является одним из важнейших «электромагнитных параметров» соответствующей среды.
Диэлектрическая проницаемость непоглощающей среды
Проницаемость и связанные с ней величины
Применительно к диэлектрической среде без потерь справедливы соотношения:
В большинстве случаев и, соответственно, — это просто безразмерные константы конкретного материала. В вакууме равно нулю.
Особая ситуация возникает для нелинейных сред, когда зависит от величины поля ; такое возможно в сравнительно сильных полях. В сегнетоэлектриках возможно появление спонтанной поляризации, а именно сохранение поляризации после снятия ранее наложенного внешнего поля.
Распределение электрического поля в пространстве с различными диэлектриками находится из численного решения уравнения Максвелла:
или уравнения Пуассона для электрического потенциала
- где обозначает плотность свободных зарядов.
На незаряженной границе двух диэлектрических сред отношение нормальных компонент напряжённости поля с обеих сторон равно обратному отношению значений проницаемости сред.
В случае однородного диэлектрика его наличие приводит к снижению электрического поля в раз, по сравнению со случаем вакуума при том же распределении свободных зарядов. Помимо закона Кулона, практически важным примером является конденсатор любой геометрии, заряд (но не разность потенциалов) обкладок которого фиксирован.
Проницаемость в оптическом диапазоне частот
Диэлектрическая проницаемость, совместно с магнитной, определяют фазовую скорость распространения электромагнитной волны в рассматриваемой среде, а именно:
Показатель преломления диэлектрика без потерь можно выразить как квадратный корень из произведения его магнитной и диэлектрической проницаемостей:
Для немагнитных сред Значения для существенного в конкретном контексте оптического диапазона могут очень сильно отличаться от статических значений: как правило, намного ниже, чем для статического поля.
Однако, если рассматривать оптический диапазон частот сам по себе, то в нём с ростом величина (а значит, и ) чаще всего возрастает. Такое поведение показателя преломления («синий свет преломляется сильнее красного») является случаем так называемой нормальной дисперсии . Противоположную ситуацию аномальную дисперсию можно наблюдать вблизи полос поглощения, но такой случай не может рассматриваться как случай без диссипативных потерь.
Тензор проницаемости анизотропных сред
Диэлектрическая проницаемость связывает электрическую индукцию и напряжённость электрического поля
В электрически анизотропных средах компонента вектора напряжённости может не только влиять на ту же самую компоненту вектора электрической индукции но и порождать другие его компоненты
В общем случае проницаемость является тензором , определяемым из следующего соотношения (в записи использовано соглашение Эйнштейна ):
или, иначе:
- где жирный шрифт использован для векторных и тензорных величин, а
— вектор напряжённости электрического поля,
- — вектор электрической индукции,
- — тензор абсолютной диэлектрической проницаемости.
В изотропном случае любая компонента вектора напряженности влияет только на при этом где символ Кронекера , поэтому уравнения Максвелла могут быть записаны с использованием скалярной диэлектрической проницаемости ( просто коэффициент в уравнении).
Статическая проницаемость некоторых диэлектриков
Значение вакуума равно единице, для реальных сред в статическом поле Для воздуха и большинства других газов в нормальных условиях значение близко к единице в силу их низкой плотности . В статическом электрическом поле для большинства твёрдых или жидких диэлектриков значение лежит в интервале от 2 до 8, для жидкой воды значение достаточно высокое, 88 при А у твердого льда больше и составляет 97 при Это объясняется тем, что переход атома Н от одного атома кислорода к другому атому вызывает перестройку ковалентных и водородных связей у обоих этих атомов кислорода и в их в окрестности. В результате вся структура ковалентных и водородных связей во льду сильно флуктуирует , и это приводит к аномально высокой поляризуемости льда, превосходя диэлектрическую проницаемость жидкой воды .
Значение велико для веществ с молекулами, обладающими большим электрическим дипольным моментом . Значение сегнетоэлектриков составляет десятки и сотни тысяч.
| Статическая диэлектрическая проницаемость материалов (таблица) | |||
|---|---|---|---|
| Вещество | Химическая формула | Условия измерения | Характерное значение ε r |
| Вакуум | - | - | 1 |
| Воздух | - | Нормальные условия , 0,9 МГц | 1,00058986 ± 0,00000050 |
| Углекислый газ | Нормальные условия | 1,0009 | |
| Тефлон (политетрафторэтилен, фторопласт) | - | 2,1 | |
| Нейлон | - | - | 3,2 |
| Полиэтилен | - | 2,25 | |
| Полистирол | - | 2,4-2,7 | |
| Каучук | - | - | 2,4 |
| Битум | - | - | 2,5-3,0 |
| Сероуглерод | - | 2,6 | |
| Парафин | - | 2,0-3,0 | |
| Бумага | - | - | 2,0-3,5 |
| Электроактивные полимеры | − | − | 2-12 |
| Эбонит | − | 2,5-3,0 | |
| Плексиглас (оргстекло) | - | - | 3,5 |
| Кварц | - | 3,5-4,5 | |
| Диоксид кремния | − | 3,9 | |
| Бакелит | - | - | 4,5 |
| Бетон | − | − | 4,5 |
| Фарфор | − | − | 4,5-4,7 |
| Стекло | − | − | 4,7 (3,7-10) |
| - | - | 4,5-5,2 | |
| Гетинакс | - | - | 5-6 |
| Слюда | - | - | 7,5 |
| Резина | − | − | 7 |
| 98 % | - | 9,7 | |
| Алмаз | Нормальные условия | 5,5-10 | |
| Поваренная соль | − | 3-15 | |
| Графит | − | 10-15 | |
| Керамика | − | − | 10-20 |
| Кремний | − | 11.68 | |
| Бор | − | 2.01 | |
| Аммиак | 20 °C | 17 | |
| 0 °C | 20 | ||
| −40 °C | 22 | ||
| −80 °C | 26 | ||
| Спирт этиловый | или | − | 27 |
| Метанол | − | 30 | |
| Этиленгликоль | − | 37 | |
| Фурфурол | − | 42 | |
| Глицерин | или | 0 °C | 41,2 |
| 20 °C | 47 | ||
| 25 °C | 42,5 | ||
| Вода | 200 °C | 34,5 | |
| 100 °C | 55,3 | ||
| 20 °C | 81 | ||
| 0 °C | 88 | ||
| Плавиковая кислота | 0 °C | 83,6 | |
| Формамид | 20 °C | 84 | |
| Серная кислота | 20-25 °C | 84-100 | |
| Пероксид водорода | −30 °C — +25 °C | 128 | |
| Синильная кислота | (0-21 °C) | 158 | |
| Диоксид титана | - | 86-173 | |
| Титанат кальция | - | 170 | |
| Титанат стронция | - | 310 | |
| Титанат бария-стронция | , | - | 500 |
| Титанат бария | (20-120 °C) | 1250-10000 | |
| Цирконат-титанат свинца | , ) | 500-6000 | |
| Сополимеры | - | - | до 100000 |
| Сульфид кадмия | 9,3 | ||
Большой диэлектрической проницаемостью обладают некоторые сложные вещества: CCTO-керамика и LSNO-керамика ( около 10 2 и 10 6 соответственно) .
Кроме того, исследуются и метаматериалы . Например диэлектрическая проницаемость порядка 10 7 —10 8 была обнаружена у металлических наноостровковых структур на диэлектрических подложках .
В электронике диэлектрическая проницаемость изоляционных материалов является одним из основных параметров для электрических конденсаторов . Применение материала с высокой диэлектрической проницаемостью позволяет существенно сократить габаритные размеры конденсатора. Например, ёмкость плоского конденсатора:
- где — относительная диэлектрическая проницаемость материала между обкладками,
- — площадь обкладок конденсатора,
- — расстояние между обкладками.
Таким образом, требуемая площадь обкладок обратно пропорциональна Значение диэлектрической проницаемости материала основания учитывается при разработке печатных плат , поскольку оно влияет на значение статической ёмкости проводящего рисунка слоёв питания и волновое сопротивление проводников ( линий передачи сигналов) на плате.
Помимо обозначения ранее для относительной диэлектрической проницаемости иногда применялось обозначение которое при отсутствии греческих шрифтов заменяли на . Это обозначение ныне почти не используется и сохранилось лишь применительно к диэлектрикам в полевых транзисторах с изолированным затвором .
Традиционно в таких приборах используется диоксид кремния (SiO 2 ). Однако в целях миниатюризации транзисторов на определённом этапе потребовался переход к материалам с более высокой, чем у SiO 2 (3,9), проницаемостью. Это позволяет получить нужную ёмкость при более толстом слое материала, что полезно, так как для тонких слоёв актуальны проблемы надёжности и туннельных утечек. Примерами применяемых подзатворных « high-k » диэлектриков являются ZrO 2 , HfO 2 (у двух названных материалов ), TiO 2 ( ) и ряд других. Микросхемы на базе транзисторов с такими материалами начали серийно выпускаться в 2000-е годы . Поиск новых подзатворных материалов продолжается.
Проницаемость диэлектрической среды с потерями
Комплексная диэлектрическая проницаемость
При описании колебаний электрического поля методом комплексных амплитуд в случае диэлектрической среды с конечной проводимостью уравнения Максвелла можно записывать по аналогии со случаем идеального диэлектрика, если ввести мнимую компоненту проницаемости.
Пусть напряженность электрического поля изменяется во времени по гармоническому закону (далее — мнимая единица ):
Тогда , а уравнение Максвелла для магнитного поля применительно к проводящей среде выглядит:
Чтобы привести это уравнение к виду, формально совпадающему с видом уравнения для непроводящей среды, величина, стоящая в скобках, интерпретируется как комплексная диэлектрическая проницаемость Значок сверху (опускаемый, если это не влечёт двусмысленности) подчеркивает, что речь идёт о комплексной величине. При наличии анизотропии становится тензорной величиной. Иногда в методе комплексных амплитуд используют зависимость вида — тогда знак перед должен быть заменён везде.
Даже в случаях, когда в постоянном электрическом поле среда обладает очень малой проводимостью, на высоких частотах могут проявиться существенные потери, которые при таком подходе приписываются некоторой «эффективной» диэлектрической проницаемости:
Наличие мнимой части связано с конечной проводимостью которая и обусловливает поглощение. Если частота изменения поля составляет , то .
Без метода комплексных амплитуд подставлять комплексную в уравнения Максвелла нельзя (следует оперировать непосредственно и ). Однако если известны и то можно воспользоваться ими для анализа свойств среды, вычисления ряда других параметров включая показатель поглощения, а также получить готовыми и для соответствующей частоты.
Характеристика диэлектрических потерь
Плотность мощности (Ватт/м 3 ) тепловыделения за счёт диэлектрических потерь составляет:
Подобный механизм разогрева широко используется в микроволновых печах. Для характеристики диэлектрика с поглощением также используется величина «тангенса угла потерь» — отношение мнимой и вещественной частей комплексной диэлектрической проницаемости:
При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол , где δ — угол диэлектрических потерь.
При отсутствии потерь δ = 0 . Тангенс угла потерь определяется отношением активной мощности к реактивной при синусоидальном напряжении заданной частоты. Величина, обратная tg δ , называется добротностью конденсатора.
При наличии поглощения взаимосвязь между компонентами комплексной проницаемости и оптическими величинами (показателями преломления и поглощения) устанавливается с использованием соотношений Крамерса — Кронига и имеет вид:
откуда для немагнитных сред следует:
Типичная частотная зависимость проницаемости
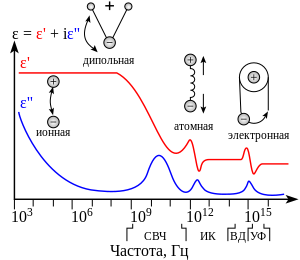
Параметры и обычно сильно зависят от частоты колебаний напряженности электрического поля. Например, ясно, что в дипольной модели поляризации процесс ориентации диполей может не успевать следовать за изменениями приложенного поля, что может проявиться как возрастанием, так и снижением проницаемости по сравнению с её статическим значением.
Наиболее типичное поведение и как функций частоты представлено на рисунке. Далеко от линий и полос поглощения («собственных частот») материала значения малы, а не изменяется или слабо растёт с частотой. В областях вблизи линий компонента имеет максимумы, а резко спадает. При этом не исключена ситуация, при которой в каком-то диапазоне окажется отрицательным или положительным, но меньше единицы. Практически является редким случаем, а ситуация на предельно высоких (рентгеновских) частотах характерна для всех материалов: в этой области с ростом подходит к единице снизу.
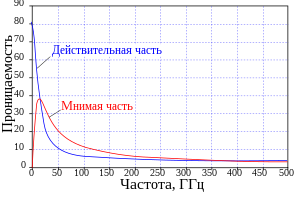
Таблицы неспециализированных справочников обычно содержат данные для статического поля или малых частот вплоть до нескольких единиц кГц (иногда даже без указания данного факта). В то же время значения в оптическом диапазоне (частота 10 14 Гц) намного отличаются в меньшую сторону от данных, представленных в подобных таблицах. Например для воды в случае статического поля относительная диэлектрическая проницаемость приблизительно равна 80. Это имеет место вплоть до инфракрасных частот. Начиная примерно с 2 ГГц (здесь ) начинает падать. В оптическом диапазоне составляет около 1,77, соответственно показатель преломления воды равен 1,33, а не квадратному корню из восьмидесяти.
Сведения о поведении относительной диэлектрической проницаемости воды в диапазоне частот от 0 до 10 12 (инфракрасная область) можно найти на (англ.).
Измерение диэлектрической проницаемости
Относительная диэлектрическая проницаемость вещества может быть определена путём сравнения ёмкости тестового конденсатора с данным диэлектриком ( ) и ёмкости того же конденсатора в вакууме ( ):
Cуществуют и оптические методы получения относительной диэлектрической проницаемости по коэффициенту преломления при помощи эллипсометров и рефрактометров .
Примечания
- Гольдштейн Л. Д., Зернов Н. В. Электромагнитные поля и волны. М.: Сов. радио, 1971. С. 11.
- Никольский В. В. , Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989. С. 35.
- Финкельштейн А. В. Физика белка / Птицын О. Б.. — 3-е изд. — М. : КДУ, 2012. — С. 45. — 456 с. — ISBN 5-98227-065-2 .
- . elementy.ru. Дата обращения: 11 февраля 2017. 11 февраля 2017 года.
-
.
из оригинала
11 февраля 2017
. Дата обращения:
11 февраля 2017
.
{{ cite news }}:|first=пропущен|last=( справка ) - . Дата обращения: 15 февраля 2017. 16 февраля 2017 года.
- Ёмкость плоского конденсатора , где d — расстояние между обкладками. Чем больше d, тем меньше ёмкость. Увеличенная проницаемость может это компенсировать.
- High-k Gate Dielectrics / Michel Houssa. — CRC Press, 2004. — 601 p. — (Series in Material Science and Engineering). — ISBN 0750309067 .
- 7 марта 2001 года.
Ссылки
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1965.
- Сивухин Д. В. Общий курс физики. — М. . — Т. III. Электричество.
- МГУ , М.: 2012 — 81 стр.
- Курс физики для ФМШ при НГУ , раздел
- 2020-01-25
- 1





































































































![{\displaystyle {\ce {[{-CF2-CF2-}]_n}}}](/images/005/764/5764055/103.jpg?rand=499239)
![{\displaystyle {\ce {[{-CH2-CH2-}]_n}}}](/images/005/764/5764055/104.jpg?rand=788818)
![{\displaystyle {\ce {[{-CH2-{(C6H5)}H-}]_{n}}}}](/images/005/764/5764055/105.jpg?rand=127583)































![{\displaystyle {\ce {(Pb[Zr_xTi_{1-x}]O3)}}}](/images/005/764/5764055/137.jpg?rand=934470)





































































