Interested Article - Теоремы об изоморфизме
- 2020-02-16
- 1

Теоремы об изоморфизме в алгебре — ряд теорем , связывающих понятия фактора , гомоморфизма и вложенного объекта . Утверждением теорем является изоморфизм некоторой пары групп , колец , модулей , линейных пространств , алгебр Ли или прочих алгебраических структур (в зависимости от области применения). Обычно насчитывают три теоремы об изоморфизме, называемые Первой (также основная теорема о гомоморфизме ), Второй и Третьей. Хотя подобные теоремы достаточно легко следуют из определения фактора и честь их открытия никому особо не приписывается, считается, что наиболее общие формулировки дала Эмми Нётер .
Группы
Первая теорема
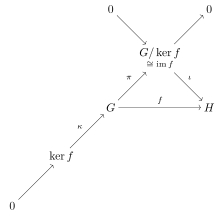
Пусть — гомоморфизм групп , тогда:
- Ядро — нормальная подгруппа в ;
- Образ — подгруппа в ;
- Образ изоморфен факторгруппе .
В частности, если гомоморфизм сюръективен (то есть является эпиморфизмом ), то группа изоморфна факторгруппе .
Вторая теорема
Пусть — группа, — подгруппа в , — нормальная подгруппа в , тогда:
- Произведение — подгруппа в ;
- Пересечение — нормальная подгруппа в ;
- Факторгруппы и изоморфны.
Третья теорема
Пусть — группа, и — нормальные подгруппы в такие, что , тогда:
- — нормальная подгруппа в ;
- Факторгруппа факторгрупп ( ) / ( ) изоморфна факторгруппе .
Кольца
В данной области понятие нормальной подгруппы заменяется на понятие идеала кольца .
Первая теорема
Пусть гомоморфизм колец , тогда:
- Ядро — идеал в ;
- Образ — подкольцо в ;
- Образ изоморфен факторкольцу .
В частности, если гомоморфизм сюръективен (то есть является эпиморфизмом), то кольцо изоморфно факторкольцу .
Вторая теорема
Пусть — кольцо, — подкольцо в , — идеал в , тогда:
- Сумма — подкольцо в ;
- Пересечение — идеал в ;
- Факторкольца и изоморфны.
Третья теорема
Пусть — кольцо, и — идеалы в такие, что , тогда:
- — идеал в ;
- Факторкольцо факторколец изоморфно факторкольцу .
Модули, абелевы группы и линейные пространства
Теоремы об изоморфизме абелевых групп и линейных пространств являются частным случаем теорем для модулей , которые и будут сформулированы. Для линейных пространств дополнительную информацию можно найти в статье « ядро линейного отображения ».
Первая теорема
Пусть — гомоморфизм модулей, тогда:
- Ядро — подмодуль в ;
- Образ — подмодуль в ;
- Образ изоморфен фактормодулю .
Вторая теорема
Пусть — модуль, и — подмодули в , тогда:
- Сумма — подмодуль в ;
- Пересечение — подмодуль в ;
- Фактормодуль изоморфен фактормодулю .
Третья теорема
Пусть — модуль, и — подмодули в такие, что , тогда:
- — подмодуль в ;
- Фактормножество фактормодулей изоморфно фактормодулю .
См. также
- 2020-02-16
- 1