Interested Article - Комбинаторная геометрия

- 2021-02-01
- 2

Комбинаторная или дискретная геометрия — раздел геометрии , в котором изучаются комбинаторные свойства геометрических объектов и связанные с ними конструкции. В комбинаторной геометрии рассматривают конечные и бесконечные дискретные множества или структуры базовых однотипных геометрических объектов ( точек , прямых , окружностей , многоугольников , тел с одинаковым диаметром , целочисленных решёток и т. п.) и ставят вопросы, связанные со свойствами различных геометрических конструкций из этих объектов или на этих структурах. Проблемы комбинаторной геометрии простираются от конкретных «предметно»-комбинаторных вопросов (хотя и не всегда с простыми ответами) — замощения , упаковка кругов на плоскости , формула Пика — до вопросов общих и глубоких, таких как гипотеза Борсука , проблема Нелсона — Эрдёша — Хадвигера .
История
Хотя многогранники , замощения и упаковка шаров исследовались ещё Кеплером и Коши , современная комбинаторная геометрия начала формироваться в конце XIX века. Одними из первых задач были: плотность упаковки кругов Акселя Туэ , Штайница , геометрия чисел Минковского и проблема четырёх красок .
Примеры задач
Представление о диапазоне задач комбинаторной геометрии дают следующие примеры.
- Лемма Витали о покрытиях — комбинаторногеометрический результат. Широко используется в теории меры.
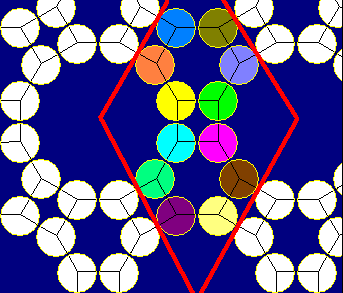
- Задача о возможных и наиболее плотных упаковках кругов на плоскости и шаров в пространстве . Наиболее плотные упаковки кругов и шаров представляются очевидными. Но полное математическое доказательство для кругов было получено только в 1940 году . Для шаров компьютерное доказательство гипотезы Кеплера появилось спустя 400 лет в 1998 году в работе математика

- Теорема Эрдёша — Секереша о выпуклых многоугольниках утверждает, что в любом достаточно большом множестве точек в общем положении на плоскости можно найти точек, являющихся вершинами выпуклого многоугольника. Гипотеза Эрдёша — Секереша о минимальном числе точек, обязательно содержащих выпуклый -угольник, на сегодня не доказана. Данная задача является также задачей теории Рамсея .
- Теорема Минковского о выпуклом теле . Пусть — замкнутое выпуклое тело , симметричное относительно начала координат -мерного евклидова пространства, имеющее объём . Тогда в найдётся целочисленная точка, отличная от . Эта теорема положила начало геометрии чисел .
- Гипотеза Борсука утверждает, что любое тело диаметра в -мерном евклидовом пространстве можно разбить на часть так, что диаметр каждой части будет меньше . Эта гипотеза была доказана для размерностей и , но опровергнута для пространств большой размерности. По известной сегодня оценке она неверна для пространств размерности 64 и более .
- Задача Данцера — Грюнбаума заключается в поиске конечного множества из как можно большего количества точек в многомерном пространстве, между которыми можно построить только острые углы.
- Задача «никакие три точки не лежат на одной прямой» , состоящая в нахождении количества точек, которые можно расположить на решётке так, чтобы никакие три точки не находились на одной прямой.
См. также
Примечания
-
Chang, Hai-Chau; Wang, Lih-Chung (2010). "A Simple Proof of Thue's Theorem on Circle Packing".
arXiv
:
[
].
{{ cite arXiv }}: Неизвестный параметр|accessdate=игнорируется ( справка ) - Thomas Jenrich, от 26 декабря 2018 на Wayback Machine
Ссылки
- Bezdek, András; Kuperberg, W. Discrete geometry: in honor of W. Kuperberg's 60th birthday (англ.) . — New York, N.Y: , 2003. — ISBN 0-8247-0968-3 .
- Bezdek, Károly. Classical Topics in Discrete Geometry (неопр.) . — New York, N.Y: Springer, 2010. — ISBN 978-1-4419-0599-4 .
- Brass, Peter; Moser, William; Research problems in discrete geometry (неопр.) . — Berlin: Springer, 2005. — ISBN 0-387-23815-8 .
- ; Agarwal, Pankaj K. (неопр.) . — New York: Wiley-Interscience , 1995. — ISBN 0-471-58890-3 .
- Goodman, Jacob E. and O'Rourke, Joseph. Handbook of Discrete and Computational Geometry, Second Edition (англ.) . — Boca Raton: Chapman & Hall/CRC, 2004. — ISBN 1-58488-301-4 .
- Gruber, Peter M. Convex and Discrete Geometry. — Berlin: Springer, 2007. — ISBN 3-540-71132-5 .
- Matoušek, Jiří. Lectures on discrete geometry. — Berlin: Springer, 2002. — ISBN 0-387-95374-4 .
- Vladimir Boltyanski, Horst Martini, Petru S. Soltan,. (неопр.) . — Springer, 1997. — ISBN 3-540-61341-2 .
- 2021-02-01
- 2