Пример парадокса: если береговая линия Великобритании измеряется отрезками по 100 км, то её длина составляет примерно 2 800 км. Если используются отрезки по 50 км, то длина равна приблизительно 3 400 км, что на 600 км больше.

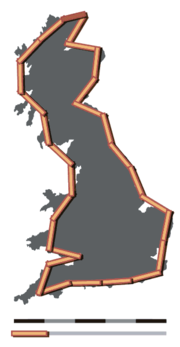
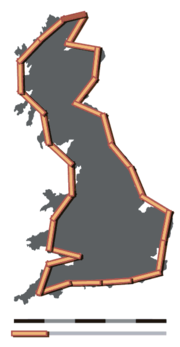
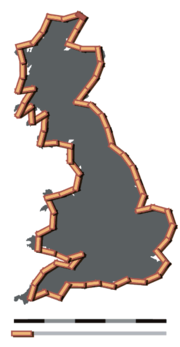
Парадокс береговой линии — противоречивое наблюдение в географических науках, связанное с невозможностью точно определить длину линии побережья из-за её фракталоподобных свойств. Первое задокументированное описание данного феномена было сделано Льюисом Ричардсоном ; впоследствии оно было расширено Бенуа Мандельбротом .

Длина береговой линии зависит от способа её измерения. Поскольку для участка суши можно выделить изгибы любого размера, от сотен километров до долей миллиметра и меньше, нельзя очевидным образом подобрать размер наименьшего элемента, который должен быть взят для измерения. Следовательно, нельзя однозначно определить и периметр данного участка. Существуют различные математические приближения при решении данной задачи.

История развития парадокса

Незадолго до 1951 года Льюис Фрай Ричардсон в ходе исследования предполагаемого влияния длины государственных границ на вероятность начала военных конфликтов заметил следующее: Португалия заявила, что её сухопутная граница с Испанией равна 987 км, а Испания определила её равной 1 214 км. Этот факт послужил отправной точкой для изучения проблемы береговой линии .

Основным методом оценки длины границы или береговой линии было наложение N равных отрезков длиной l на карту или аэрофотоснимок с помощью циркуля. Каждый конец отрезка должен принадлежать измеряемой границе. Исследуя расхождения в оценке границ, Ричардсон обнаружил то, что сейчас называется эффектом Ричардсона : масштаб измерений обратно пропорционален общей длине всех отрезков. То есть чем короче используемая линейка, тем длиннее измеряемая граница. Таким образом, испанские и португальские географы попросту руководствовались измерениями разных масштабов.

Наиболее поразительным для Ричардсона оказалось то, что когда величина l стремится к нулю, длина побережья стремится к бесконечности. Изначально Ричардсон полагал, опираясь на евклидову геометрию, что эта длина достигнет фиксированной величины, как это происходит в случае с правильными геометрическими фигурами. Например, периметр правильного многоугольника, вписанного в окружность, приближается к длине самой окружности с увеличением числа сторон (и уменьшением длины каждой стороны). В теории геометрических измерений такая гладкая кривая, как окружность, которая может быть приближённо представлена в виде небольших отрезков с заданным пределом, называется спрямляемой кривой.

Спустя более десяти лет после завершения Ричардсоном своей работы Мандельброт разработал новую ветвь математики — фрактальную геометрию — для описания таких неспрямляемых комплексов, существующих в природе, как бесконечная береговая линия . Его собственное определение фрактала как основы его исследования таково :

Я придумал слово фрактал , взяв за основу латинское прилагательное fractus . Соответствующий латинский глагол frangere означает ломать : создавать нерегулярные фрагменты. Поэтому разумно, что, помимо «фрагментный», fractus также должно означать и «нерегулярный».

Ключевым свойством фракталов является самоподобие , заключающееся в проявлении одной и той же общей фигуры на любом масштабе. Береговая линия воспринимается как чередование заливов и мысов. Гипотетически, если данная береговая линия имеет свойство самоподобия, то независимо от того, насколько сильно масштабируется та или иная часть, всё равно проявляется аналогичная картина меньших заливов и мысов, наложенная на бо́льшие заливы и мысы, вплоть до песчинок. На таких масштабах береговая линия оказывается мгновенно изменяющейся, потенциально бесконечной нитью со стохастическим расположением заливов и мысов. В таких условиях (в отличие от гладких кривых) Мандельброт утверждает: «Длина береговой линии оказывается недостижимым понятием, скользящим между пальцами тех, кто пытается его понять» .

Математическая интерпретация

Понятие длины происходит от Евклидового расстояния . В евклидовой геометрии прямая линия представляет собой кратчайшее расстояние между двумя точками . Геодезическая линия на поверхности сферы, называемая большим кругом , измеряется вдоль кривой, которая лежит в плоскости, содержащей конечные точки пути и центр сферы. Длина кривой вычисляется более сложно. При использовании линейки длину кривой можно приблизительно вычислить, суммируя длины отрезков, соединяющих точки:

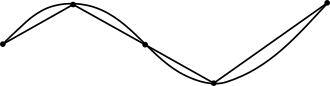
Использование всё более коротких отрезков будет давать всё более точное значение, приближающееся к реальному значению длины дуги. Такое точное значение для бесконечно малых расстояний можно вычислить с помощью математического анализа . Следующая анимация показывает, насколько гладкой может быть подобная кривая с точным значением длины:

Однако не все кривые могут быть измерены подобным способом. Фрактал имеет разную сложность в зависимости от масштаба, поэтому измеряемые значения длин фракталов могут непредсказуемо меняться.

Кривая Серпинского , повторяющая один и тот же рисунок на всё меньших масштабах, продолжает увеличиваться в длине. Если рассматривать итерации в бесконечно делимом геометрическом пространстве, её длина стремится к бесконечности. В то же время площадь фигуры, ограниченной данной кривой, стремится к определённому значению — аналогично тому, что площадь острова измеряется гораздо легче, чем длина его береговой линии.

Длина «истинного фрактала» всегда стремится к бесконечности, так же как и длины бесконечно малых изгибов береговой линии суммируются до бесконечности . Но это утверждение основано на предположении о неограниченности пространства, которое, в свою очередь, вряд ли отражает реальную концепцию пространства и расстояния на атомном уровне. Наименьшей единицей измерения длины во Вселенной считается планковская длина , намного меньшая размеров атома.

Береговая линия со свойством самоподобия входит в «первую категорию фракталов, а именно является кривой с фрактальной размерностью больше 1». Это последнее утверждение представляет собой расширение Мандельбротом мысли Ричардсона. Мандельброт так формулирует эффект Ричардсона :

${\displaystyle L(\epsilon )\sim F\epsilon ^{1-D}}$

где длина береговой линии L является функцией от единицы измерения ε и аппроксимируется выражением из правой части. F — константа, D — параметр Ричардсона, зависящий от самой береговой линии (Ричардсон не дал теоретического объяснения этой величины, однако Мандельброт определил D как нецелочисленную форму размерности Хаусдорфа , позже — фрактальной размерности. Иными словами, D — это практически измеренное значение «неровности»). Перегруппировав правую часть выражения, получаем:

${\displaystyle {\frac {F}{\epsilon ^{D}}}\cdot \epsilon }$

где Fε ^-D должно быть количеством единиц ε, необходимых для получения L. Фрактальная размерность — это число измерений объекта, используемое для аппроксимации фрактала: 0 — для точки, 1 — для линии, 2 — для площадных фигур. Поскольку ломаная линия, измеряющая длину берега, не распространяется в одном направлении и вместе с тем не представляет собой площадь, значение D в выражении занимает промежуточное положение между 1 и 2 (для побережья обычно менее 1,5). Оно может быть интерпретировано как толстая линия или полоса шириной 2ε. Более «разбитые» побережья имеют большее значение D и тем самым L оказывается длиннее при одинаковых ε. Мандельброт показал, что D не зависит от ε.

В целом береговые линии отличаются от математических фракталов, поскольку они формируются с использованием многочисленных мелких деталей, создающих модели только статистически .

Парадокс на практике

Из практических соображений выбирают минимальный размер деталей равным порядку единиц измерения. Так, если береговая линия измеряется в километрах, то небольшие изменения линий, гораздо меньшие одного километра, просто не принимаются во внимание. Для измерения береговой линии в сантиметрах должны быть рассмотрены все небольшие вариации размером около одного сантиметра. Однако на масштабах порядка сантиметров должны быть сделаны различные произвольные нефрактальные допущения, например, там, где устье присоединяется к морю, или в тех местах, где должны быть проведены измерения на широких ваттах . Кроме того, использование различных методов измерения для разных единиц измерения не позволяет сделать преобразование этих единиц с помощью простого умножения.

Для определения государственных территориальных вод строят так называемые прямые исходные линии , соединяющие официально установленные точки побережья. Длину такой официальной береговой линии тоже не составляет труда измерить.

Предельные случаи парадокса береговой линии включают побережья с большим числом фьордов : это побережья Норвегии , Чили , северо-западное побережье Северной Америки и другие. От южной оконечности острова Ванкувер в северном направлении до южной оконечности Юго-Восточной Аляски изгибы побережья канадской провинции Британская Колумбия составляют более 10 % длины канадской береговой линии (с учётом всех островов Канадского Арктического архипелага ) — 25 725 км из 243 042 км на линейном расстоянии, равном всего 965 км .

См. также

• Фрактальная размерность
• Парадокс кучи
• Апории Зенона
• Спор о границе Аляски
• « Какова длина побережья Великобритании? »

Примечания

Дополнительная литература

• Michael Frame, Benoit Mandelbrot, and Nial Neger. (англ.) . Fractals . yale.edu. Дата обращения: 13 февраля 2016.
• II.5 How long is the coast of Britain? // The Fractal Geometry of Nature. — Macmillan, 1983. — P. 25—33. — ISBN 978-0-7167-1186-5 .
• (англ.) . NOAA GeoZone Blog on Digital Coast . geozoneblog.wordpress.com (26 марта 2012). Дата обращения: 13 февраля 2016.