Числа Бернулли
- 1 year ago
- 0
- 0
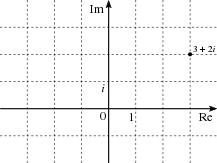
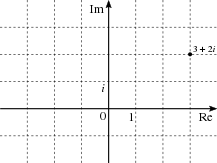
Га́уссовы це́лые чи́сла ( гауссовы числа , целые комплексные числа ) — это комплексные числа , у которых как вещественная, так и мнимая часть — целые числа .
Примеры: .
Впервые введены Гауссом в монографии «Теория биквадратичных вычетов» (1828—1832) . Множество гауссовых целых чисел принято обозначать отражая тем самым тот факт, что оно получается из множества целых чисел добавлением в него мнимой единицы и комбинаций её с целыми числами. Свойства гауссовых чисел похожи на свойства обычных целых чисел, однако имеются и существенные отличия.
Формальное определение:
Множество содержит множество обычных целых чисел и представляет собой его расширение . Сумма, разность и произведение гауссовых чисел являются гауссовыми числами; для них, как и для целых чисел, сохраняются свойства ассоциативности , коммутативности и дистрибутивности — такая алгебраическая структура называется в общей алгебре коммутативным кольцом . Ввести в этом комплексном кольце упорядоченность , согласованную с порядком вещественных чисел , невозможно.
Сопряжённое к гауссовому числу есть также гауссово число .
Каждое гауссово число удовлетворяет квадратному уравнению:
Поэтому гауссово число есть целое алгебраическое число .
Норма для гауссова числа определяется как квадрат его модуля :
Свойства нормы :
Норма, как и модуль, обладает важным свойством мультипликативности :
Отсюда следует , что обратимыми элементами кольца ( делителями единицы ) являются те элементы, у которых норма равна 1, то есть .
Два гауссовых числа называются ассоциированными, если одно получается из другого умножением на делитель единицы. Легко видеть, что ассоциированность — отношение эквивалентности . Пример: гауссовы числа и ассоциированы, поскольку:
У каждого ненулевого гауссова числа есть три ассоциированных с ним. Нормы всех четырёх ассоциированных между собой чисел совпадают.
Деление нацело гауссовых чисел определяется обычным образом :
|
Говорят, что гауссово число делится (нацело) на гауссово число , если существует третье гауссово число такое, что . Обозначение: . |
Произношение: один из трёх равносильных вариантов.
Используются традиционные термины: делимое или кратное ( ), делитель ( ) и частное от деления ( ). Количество делителей гауссова числа всегда конечно, количество кратных бесконечно.
Пример: число 2 делится нацело на , потому что .
Все гауссовы числа делятся на делители единицы, поэтому любое гауссово число, отличное от делителей единицы, имеет как минимум 8 делителей: 4 делителя единицы и 4 их произведения на само это число. Эти делители называются тривиальными .
Деление нацело в по своим свойствам похоже на аналогичное деление целых чисел. Некоторые специфические для гауссовых чисел особенности :
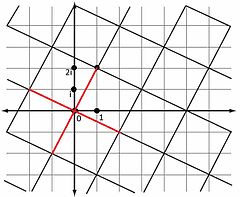
У каждого гауссова числа есть 4 кратных с той же нормой (и, соответственно, тем же модулем) — это само и ассоциированные с ним 3 числа, которые получаются последовательным умножением на :
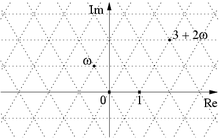
Но умножение на означает на комплексной плоскости поворот радиус-вектора числа на 90° против часовой стрелки, причём модуль результата будет тем же. Таким образом, все 4 числа образуют равносторонний крест (выделен красным на рисунке), центр и вершины которого кратны . Последовательно сдвигая этот крест во все стороны на одну из 4 величин, ассоциированных с , мы получаем на всей плоскости квадратную решётку, все узлы которой (вершины квадратов) кратны . Обратно, любое кратное совпадает с одним из узлов решётки. Ширина каждого квадрата решётки равна . Далее для краткости эта решётка будет называться «решёткой кратных» (или, если требуется уточнение, « -решёткой кратных »).
Пример: на рисунке одним из узлов решётки является число , кратное :


Простое гауссово число — это ненулевое число, не имеющее других делителей, кроме тривиальных. Число, не являющееся простым, называется составным . При этом делители единицы, подобно натуральной единице, не считаются ни простыми, ни составными числами .
Некоторые свойства простых гауссовых чисел:
Натуральное простое число может не быть гауссовым простым числом. Например, числа 2 и 5 в уже не простые:
Разложение гауссовых чисел с нормой от 2 до 100 на простые гауссовы множители см. в таблице Факторизация гауссовых чисел .
Если гауссово число является делителем для двух гауссовых чисел и , оно называется их общим делителем. Множество общих делителей двух чисел всегда содержит 4 делителя единицы; если других общих делителей нет, эти числа называются взаимно простыми .
Отметим, что если нормы гауссовых чисел взаимно просты как целые числа, то и сами числа взаимно просты как гауссовы числа. Обратное неверно: нормы взаимно простых гауссовых чисел могут иметь общие делители — например, и взаимно просты, но их нормы совпадают и поэтому не взаимно просты.
Укажем два свойства, аналогичные свойствам целых чисел.
Гаусс указал определяющие признаки простого числа в .
|
Гауссово число является простым тогда и только тогда, когда:
|
Примеры простых гауссовых чисел:
Некоторые источники для большей ясности разделяют вторую часть критерия на две :
Сам Гаусс такого разделения не делал .
Следствия:
В имеет место аналог основной теоремы арифметики : каждое гауссово число, не являющееся нулём или делителем единицы, разлагается на простые множители, причём это разложение однозначно с точностью до порядка и ассоциированности множителей .
Пример: . Множители этих двух, по виду разных, разложений попарно ассоциированы: так что однозначность не нарушается.
Чтобы практически разложить гауссово число на простые множители, можно использовать приведённое выше свойство: все делители гауссова числа являются также делителями его нормы. При этом норма содержит также «лишние» простые множители, соответствующие сопряжённому к числу.
Таким образом, начать следует с разложения нормы числа на простые натуральные множители .
Например, для разложения на простые множители (норма — 225) выделяются простые натуральные множители: . По предыдущему, . При этом делится только на и не делится на . Частное от деления на равно поэтому окончательный результат:
Понятие сравнения по модулю определяется в аналогично тому, как это делается для целых чисел :
|
Пусть — некоторое гауссово число. Два гауссовых числа называются сравнимыми по модулю , если разность делится (нацело) на . Запись: . |
Свойства сравнений в в основном такие же, как у целых чисел. Отношение сравнимости есть отношение эквивалентности , поэтому разбивается на непересекающиеся классы вычетов — каждый такой класс содержит все сравнимые друг с другом (по заданному модулю) гауссовы числа. Для классов, как в случае целых чисел, можно определить сложение и умножение, так что получается кольцо вычетов по гауссову модулю.
Пример. Возьмём в качестве модуля сравнения . Тогда разбивается на два класса вычетов: числа , у которых одинаковой чётности, попадут в один класс (содержащий кратные для модуля), а числа с разной чётностью — в другой.
У гауссова сравнения имеются некоторые особенности. Например, если для целых чисел по модулю 3 существуют 3 класса вычетов с представителями то для гауссовых чисел по тому же модулю количество классов значительно больше. Их представители:
Как обнаружил Гаусс, кольцо вычетов по модулю содержит элементов . Этот факт вынуждает модифицировать некоторые классические теоремы. Например, малая теорема Ферма для целых чисел утверждает, что делится на для любого простого и натурального . Для гауссовых чисел это неверно, даже если ограничиться натуральными значениями ; например, для целых чисел всегда делится на 3, а для гауссовых , и это значение на 3 не делится. Модифицированный аналог малой теоремы Ферма формулируется следующим образом :
Для простого гауссова числа и любого гауссова числа
делится на .
На том же примере с результат: — делится на 3.
Назовём класс вычетов по модулю содержащий число обратимым , если сравнение имеет решение относительно . Класс обратим тогда и только тогда, когда гауссовы числа и взаимно просты . В частности, если модуль сравнений — гауссово простое число, то каждый ненулевой класс вычетов имеет обратный элемент, а это значит, что классы вычетов по простому модулю в , как и в образуют поле .
Введём аналог функции Эйлера для гауссовых чисел. Определение для целых чисел не годится хотя бы потому, что содержащееся в нём выражение «от до » не имеет смысла для комплексных чисел. Новое определение :
|
Функция Эйлера для гауссова числа определяется как число обратимых классов вычетов по модулю . |
Определённая таким образом функция, как и её прототип для целых чисел, мультипликативна , поэтому достаточно знать её значения для простых чисел и их натуральных степеней. Если — простое гауссово число, то :
Пример: .
Теперь можно обобщить приведённую в предыдущем разделе малую теорему Ферма на случай произвольного (не обязательно простого) модуля сравнения, то есть привести аналог теоремы Эйлера :
|
Если гауссово число
взаимно просто с модулем
, то:
|
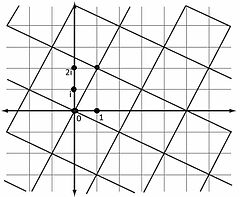
Рассмотрим для примера сравнения по модулю . Как сказано в разделе о геометрическом представлении делимости, можно разбить комплексную плоскость на квадраты так, что узлы этой решётки (вершины квадратов) представляют всевозможные комплексные кратные . Тогда, по определению, числа сравнимы по модулю , если их разность совпадает с одним из узлов решётки кратных.
Каждый квадрат решётки получается из любого другого квадрата сдвигом (переносом) на величину, кратную поэтому разность любой точки квадрата и результата её сдвига тоже кратна . Отсюда следует окончательный вывод :
|
Гауссовы числа сравнимы по модулю тогда и только тогда, когда они занимают одно и то же относительное положение в своих квадратах решётки кратных. |
Например, сравнимы все центры квадратов, или все середины их соответствующих сторон и т. п.
В кольце можно определить деление с остатком (на любое ненулевое гауссово число), потребовав, чтобы норма остатка была меньше нормы делителя :
|
Любое гауссово число можно разделить с остатком на любое ненулевое гауссово число , то есть представить в виде: где частное и остаток — гауссовы числа, причём . |
Несложно показать, что в качестве частного от деления с остатком можно взять гауссово число, ближайшее к частному от обычного деления комплексных чисел .
Необходимо отметить, что условия «норма остатка меньше нормы делителя» недостаточно для того, чтобы гарантировать однозначность остатка от деления, поэтому в остаток неоднозначен. Например, можно разделить на тремя способами:
Можно гарантировать только то, что все остатки попадают в один класс вычетов по модулю делителя. Впрочем, похожая ситуация имеет место и для обычных целых чисел — например, разделить с остатком 8 на 3 можно двумя способами: или (оба остатка по модулю меньше делителя) поэтому в арифметике целых чисел введено дополнительное условие, обеспечивающее однозначность операции: остаток должен быть неотрицательным.
Пример . Для деления с остатком на вначале находится частное от обычного комплексного деления:
Ближайшее к результату гауссово число есть тогда остаток равен . В итоге:
Для гауссовых чисел имеет место аналог китайской теоремы об остатках , поскольку она доказывается с помощью алгоритма Евклида .
Из определения деления с остатком на следует, что , то есть модуль остатка есть расстояние между комплексными числами и . Другими словами, есть расстояние от делимого до одного из узлов -решётки кратных. Требование «норма остатка меньше нормы делителя» эквивалентно условию . Отсюда вытекает:
|
Деление с остатком на имеет столько решений, сколько узлов -решётки кратных находится от делимого на расстоянии меньше . |
В вышеприведённом примере деления на ближайшими к делимому являются кратные делителя, образующие вершины квадрата решётки, содержащего делимое:
Все они находятся от делимого на расстоянии меньше, чем . Четвёртая вершина квадрата удалена от делимого больше чем на . Поэтому данная задача деления с остатком имеет три решения.
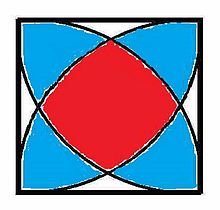
В общем случае, проведя из вершин квадрата -решётки кратных дуги радиусом мы получим фигуру, показанную на рисунке. Если делимое находится в центральной области (красная зона), оно удалено от всех вершин менее чем на и деление с остатком может быть выполнено четырьмя способами. Если делимое находится в одном из «лепестков» (синяя зона), то одна из вершин отпадает, и число решений равно трём. Для белой зоны получаем два решения. Наконец, если делимое совпадает с одной из вершин, то остаток равен нулю, и решение единственно.
Кольцо гауссовых чисел является евклидовым , и в нём всегда можно определить наибольший общий делитель , определённый однозначно с точностью до делителей единицы .
|
Наибольшим общим делителем НОД для гауссовых чисел и , хотя бы одно из которых ненулевое, называется их общий делитель, который делится на любой другой общий делитель и . |
Эквивалентное определение: НОД есть тот общий делитель , у которого норма максимальна .
|
Пусть — гауссовы числа, и хотя бы одно из них не нуль. Тогда существуют такие гауссовы числа , что выполняется соотношение:
|
Для определения НОД в удобно использовать алгоритм Евклида , вполне аналогичный применяемому для целых чисел. НОД получается в этой схеме как последний ненулевой остаток . Алгоритм Евклида можно также использовать для нахождения коэффициентов в соотношении Безу .
Пример 1. Найдём НОД для и .
Отметим, что на каждом шаге норма остатка монотонно уменьшается. Последний ненулевой остаток равен , это делитель единицы, поэтому заключаем, что исследуемые числа взаимно просты.
Пример 2. Найдём НОД для и .
Последний ненулевой остаток равен , это и есть искомый НОД. Последовательно подставляя вместо левых частей равенств правые (начиная с предпоследнего равенства, снизу вверх), получается соотношение Безу для НОД:
Гаусс использовал открытую им алгебраическую структуру для глубокого исследования биквадратичных вычетов. Можно указать и другие области успешного применения гауссовых чисел . Примечательно, что значительная их часть относится к теории не комплексных, а натуральных чисел.
Из критерия Гаусса вытекает, что простое натуральное число вида можно представить в виде суммы квадратов двух натуральных чисел, причём единственным способом. Пример: .
Разложение натуральных чисел другого вида не всегда возможно — например, и другие числа вида нельзя представить в виде суммы квадратов двух натуральных чисел. Составные числа могут также иметь более одного варианта разложения, например : . Общая теорема: натуральное число представимо в виде суммы двух квадратов тогда и только тогда, когда в его каноническом разложении все простые множители вида входят в чётных степенях .
Пример: нельзя представить в виде суммы квадратов, потому что число 3 (как и 7) входит в него с нечётной степенью. Но представить можно: .
Число представлений натурального числа в виде суммы квадратов (или, что то же самое, число гауссовых чисел с нормой ) можно определить следующим образом . Разложим на простые натуральные множители:
Здесь — множители вида а — множители вида . Тогда возможны 3 случая.
Пифагорова тройка — это одно из целочисленных решений уравнения:
Общее решение уравнения зависит от двух целых параметров :
Для генерации пифагоровых троек можно использовать такой приём. Пусть — произвольное гауссово число, у которого обе компоненты ненулевые. Возведя это число в квадрат, получается некоторое другое гауссово число . Тогда тройка будет пифагоровой .
Пример: для исходного числа получается пифагорова тройка .
Решение многих диофантовых уравнений удаётся найти, если привлечь аппарат гауссовых чисел. Например, для уравнения несложные преобразования дают два типа целых взаимно простых решений , зависящих от целых параметров :
В 1850 году Виктор Лебег, используя гауссовы числа, исследовал уравнение и доказал его неразрешимость в натуральных числах. Другими словами, среди натуральных чисел вида нет ни одного полного куба или иной степени выше второй .
Ещё одним исторически важным евклидовым кольцом, похожим по свойствам на целые числа, стали « целые числа Эйзенштейна ».
Гауссовы рациональные числа, обозначаемые — это комплексные числа вида , где — рациональные числа . Это множество замкнуто относительно всех 4 арифметических операций, включая деление, и поэтому является полем , расширяющим кольцо гауссовых чисел.
В 1820-х годах Карл Фридрих Гаусс исследовал биквадратичный закон взаимности , результатом стала монография «Теория биквадратичных вычетов» (1828—1832). Именно в этом труде целые комплексные числа доказали свою полезность для решения задач теории чисел , хотя формулировка этих задач никак не связана с комплексными числами. Гаусс писал, что «естественный источник общей теории следует искать в расширении области арифметики» .

В книге Гаусса было показано, что новые числа по своим свойствам во многом напоминают обычные целые числа. Автор описал четыре делителя единицы , определил отношение ассоциированности, понятие простого числа, дал критерий простоты и доказал аналоги основной теоремы арифметики , малой теоремы Ферма . Далее Гаусс подробно рассмотрел вычеты по комплексному модулю, индексы и первообразные корни . Главным достижением построенной теории стал биквадратичный закон взаимности, который Гаусс обещал доказать в следующем томе; этот том так и не был опубликован, но в рукописях Гаусса была обнаружена подробная схема строгого доказательства .
Гаусс использовал введённые им числа также и в других своих трудах, например, по алгебраическим уравнениям . Идеи Гаусса были развиты в трудах Карла Густава Якоба Якоби и Фердинанда Готтхольда Эйзенштейна . В середине XIX века Эйзенштейн, Дирихле и Эрмит ввели и исследовали обобщённое понятие целого алгебраического числа .
Кольцо гауссовых целых чисел было одним из первых примеров алгебраической структуры с непривычными свойствами. Со временем было открыто большое количество структур такого типа, а в конце XIX века появилась абстрактная алгебра , изучающая алгебраические свойства отдельно от объектов-носителей этих свойств.