Кватернионы предоставляют удобное математическое обозначение ориентации пространства и вращения объектов в этом пространстве.

В сравнении с углами Эйлера кватернионы позволяют проще комбинировать вращения, а также избегают проблемы, известной как складывание рамок : при тангаже 90° крен и курс — одно и то же движение.

В сравнении с матрицами поворота они не страдают от (любой ненулевой кватернион превращается в кватернион вращения простым нормированием), позволяют анимировать поворот кратчайшим путём без побочных эффектов вроде «конфетного фантика», и могут быть более эффективными.

Кватернионы нашли своё применение в компьютерной графике , робототехнике , навигации , молекулярной динамике .

Операции вращения

Представление пространства вращения

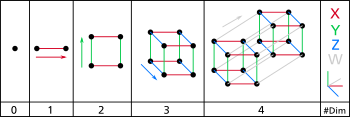
Кватернионы единичной нормы , согласно Гамильтону называемые также версорами ( англ. versors ), предоставляют алгебраический способ представления вращения в трёх измерениях. Соответствие между вращениями и кватернионами в первую очередь может быть осознано через само пространство вращения — группу SO(3) .

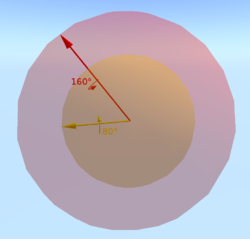
Любое вращение в трёхмерном пространстве — это вращение на определённый угол вокруг определённой оси. Если угол равен нулю, то выбор оси не имеет значения; таким образом, вращения на угол 0° — это точка в пространстве вращения ( тождественное вращение). Для крошечного (но ненулевого) угла каждое возможное вращение на этот угол — это маленькая сфера , окружающая тождественное вращение, где каждая точка на этой сфере представляет собой ось, указывающую в определённом направлении (можно сравнить с небесной сферой ). Чем больше угол вращения, тем дальше вращение от тождественного вращения; о таких вращениях можно думать как о концентрических сферах с увеличивающимся радиусом. Таким образом, вблизи тождественного вращения абстрактное пространство вращений выглядит как обычное трёхмерное пространство (которое также можно представить как центральную точку, окружённую концентрическими сферами). При увеличении угла до 360° вращения вокруг различных осей перестают расходиться и начинают становиться похожими друг на друга, становясь равными тождественному вращению, когда угол достигает 360°.

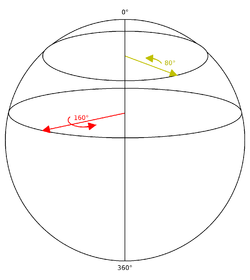
Мы можем увидеть похожее поведение на поверхности сферы. Если мы расположимся на северном полюсе и начнём чертить прямые линии, исходящие из него в различных направлениях (то есть линии долготы ), то сначала они будут расходиться, но затем снова сойдутся на южном полюсе. Концентрические круги, получившиеся вокруг северного полюса ( широты ), стянутся в одну точку на южном полюсе — когда радиус сферы сравняется с расстоянием между полюсами. Если думать о разных направлениях из полюса (то есть разные долготы) как о разных осях вращения, а о разных расстояниях от полюса (то есть широтах) как о разных углах вращения, то мы получим пространство для вращений. Получившаяся сфера представляет вращение в трёхмерном пространстве, хотя является двухмерной поверхностью, что не позволяет смоделировать гиперсферу . Однако двухмерную поверхность сферы можно представлять как часть гиперсферы (как окружность является частью сферы). Мы можем взять часть, например, для представления вращения вокруг осей в плоскости xy . Важно отметить, что угол вращения до экватора равен 180° (а не 90°); до южного полюса (с северного) 360° (а не 180°).

Северный и южный полюс представляют одинаковые вращения. Это справедливо для двух любых диаметрально противоположных точек: если одна точка — это вращение на угол ${\displaystyle \alpha }$ вокруг оси v , то диаметрально противоположной является точка с вращением на угол ${\displaystyle \scriptstyle 360^{\circ }-\alpha }$ вокруг оси − v . Таким образом, пространство вращений является не самой 3-сферой , а 3- полу сферой ( шаром на ней радиуса ${\displaystyle \pi }$ ) с отождествлёнными диаметрально противоположными точками, что диффеоморфно проективному пространству ${\displaystyle \mathbb {R} \mathrm {P} ^{3}}$ . Однако для большинства целей можно думать о вращениях как о точках на сфере несмотря на то, что они обладают двойной избыточностью.

Определение пространства вращения

Координаты точки на поверхности сферы можно задать двумя числами, например широтой и долготой. Однако такая координата, как долгота, на северном и южном полюсах начинает вести себя неопределённо (проявляет вырожденность ), хотя северный и южный полюса принципиально не отличаются от любой другой точки поверхности сферы. Это показывает, что ни одна координатная система не может двумя координатами охарактеризовать положение в пространстве. Этого можно избежать, поместив сферу в трёхмерное пространство, охарактеризовав её декартовыми координатами ( w , x , y ), помещая северный полюс на ( w , x , y ) = (1, 0, 0), южный полюс на ( w , x , y ) = (−1, 0, 0), а экватор на w = 0, x ² + y ² = 1. Точки на сфере удовлетворяют отношению w ² + x ² + y ² = 1. В итоге получаются две степени свободы , хотя имеется три координаты. Точка ( w , x , y ) представляет вращение вокруг оси ( x , y , 0) на угол ${\displaystyle \alpha =2\arccos w=2\arcsin {\sqrt {x^{2}+y^{2}}}}$ .

Таким же образом пространство трёхмерных вращений может быть охарактеризовано тремя углами ( углами Эйлера ), однако любое такое представление начинает вырождаться на некоторых точках гиперсферы. Этой проблемы можно избежать, используя евклидовы координаты w , x , y , z , где w ² + x ² + y ² + z ² = 1. Точка ( w , x , y , z ) представляет вращение вокруг осей ( x , y , z ) на угол ${\displaystyle \alpha =2\arccos w=2\arcsin {\sqrt {x^{2}+y^{2}+z^{2}}}.}$

Коротко о кватернионах

Комплексное число может быть определено введением абстрактного символа i , который удовлетворяет обычным правилам алгебры, а также правилу ${\displaystyle i^{2}=-1}$ . Этого достаточно для воспроизведения всех правил арифметики комплексных чисел. Например:

${\displaystyle (a+b\mathbf {i} )(c+d\mathbf {i} )=ac+ad\mathbf {i} +b\mathbf {i} c+b\mathbf {i} d\mathbf {i} =ac+ad\mathbf {i} +bc\mathbf {i} +bd\mathbf {i} ^{2}=(ac-bd)+(bc+ad)\mathbf {i} }$ .

Таким же образом кватернионы могут быть определены введением абстрактных символов i , j , k , умножение которых задаются по правилу

${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i} \mathbf {j} \mathbf {k} =-1}$

${\displaystyle \mathbf {i} \mathbf {j} =-\mathbf {j} \mathbf {i} =\mathbf {k} }$

${\displaystyle \mathbf {j} \mathbf {k} =-\mathbf {k} \mathbf {j} =\mathbf {i} }$

${\displaystyle \mathbf {k} \mathbf {i} =-\mathbf {i} \mathbf {k} =\mathbf {j} }$

а умножение на вещественные числа определяются обычным образом, причём умножение полагается ассоциативным , но не коммутативным (примером некоммутативного умножения является также умножение матриц ). Из этого следуют все правила кватернионной арифметики, например

${\displaystyle (a+b\mathbf {i} )(e+h\mathbf {k} )=ae+be\mathbf {i} -bh\mathbf {j} +ah\mathbf {k} }$ .

Мнимая часть ${\displaystyle b\mathbf {i} +c\mathbf {j} +d\mathbf {k} }$ кватерниона ведёт себя так же, как и вектор ${\displaystyle (b,c,d)\in \mathbb {R} ^{3}}$ , а вещественная часть a ведёт себя так же, как и скаляр в ${\displaystyle \mathbb {R} }$ . При использовании кватернионов можно, следуя Гамильтону, описывать их как сумму скаляра и вектора и использовать векторное и скалярное произведения ${\displaystyle \times }$ и ${\displaystyle \cdot }$ (идея которых была подсказана кватернионами). При этом они связаны с обычным кватернионным умножением следующей формулой:

${\displaystyle \mathbf {v} \times \mathbf {w} =\mathbf {vw} +\mathbf {v} \cdot \mathbf {w} }$ .

Векторное произведение некоммутативно, а произведения скаляр—скаляр и скаляр—вектор коммутативны. Из этих правил следует:

${\displaystyle (s+\mathbf {v} )(t+\mathbf {w} )=(st-\mathbf {v} \cdot \mathbf {w} )+(s\mathbf {w} +t\mathbf {v} +\mathbf {v} \times \mathbf {w} )}$ .

Обратным (слева и справа) для ненулевого кватерниона ${\displaystyle s+\mathbf {v} }$ является

${\displaystyle (s+\mathbf {v} )^{-1}={\frac {s-\mathbf {v} }{s^{2}+|\mathbf {v} |^{2}}}}$ ,

что может быть проверено прямым вычислением.

Определение пространства вращения через кватернионы

Допустим ( w , x , y , z ) — координаты вращения, согласно прежнему описанию. Тогда кватернион q можно определить как

${\displaystyle q=w+x\mathbf {i} +y\mathbf {j} +z\mathbf {k} =w+(x,y,z)=\cos(\alpha /2)+\mathbf {u} \sin(\alpha /2)}$ ,

где ${\displaystyle \mathbf {u} }$ — единичный вектор. Таким образом, произведение

${\displaystyle q\mathbf {v} q^{-1}}$

вращает вектор ${\displaystyle \mathbf {v} }$ на угол ${\displaystyle \alpha }$ вокруг оси заданной вектором ${\displaystyle \mathbf {u} }$ . Вращение происходит по часовой стрелке , если рассматривать вращение по направлению вектора ${\displaystyle \mathbf {u} }$ ; то есть, направление вектора ${\displaystyle \mathbf {u} }$ совпадает с направлением поступательного движения правого винта , когда он проворачивается на положительный угол ${\displaystyle \alpha }$ .

Можно взять композицию вращений на кватернионы, перемножив их (от порядка умножения зависит порядок вращения). Таким образом, вращения на кватернионы ${\displaystyle p}$ и ${\displaystyle q}$ равно

${\displaystyle pq\mathbf {v} (pq)^{-1}=pq\mathbf {v} q^{-1}p^{-1}}$

что то же самое, что и вращение на ${\displaystyle q}$ , а затем на ${\displaystyle p}$ .

Обращение кватерниона — это то же, что и вращение в противоположном направлении, таким образом ${\displaystyle q^{-1}(q\mathbf {v} q^{-1})q=\mathbf {v} }$ . Квадрат кватерниона — это вращение на двойной угол вокруг той же оси. В общем смысле, ${\displaystyle q^{n}}$ — это вращение вокруг оси ${\displaystyle q}$ на угол в ${\displaystyle n}$ раз больший первоначального. Вместо ${\displaystyle n}$ может быть любое вещественное число ^{[ источник не указан 3248 дней ]} , позволяя использовать кватернионы для плавной интерполяции между двумя положениями в пространстве.

Вращение на единичный кватернион

Пусть u — это единичный вектор (ось вращения), а ${\displaystyle q=\cos {\frac {\alpha }{2}}+\mathbf {u} \sin {\frac {\alpha }{2}}}$ кватернион. Наша цель — показать, что

${\displaystyle \mathbf {v} '=q\mathbf {v} q^{-1}=\left(\cos {\frac {\alpha }{2}}+\mathbf {u} \sin {\frac {\alpha }{2}}\right)\,\mathbf {v} \,\left(\cos {\frac {\alpha }{2}}-\mathbf {u} \sin {\frac {\alpha }{2}}\right)}$

вращает вектор v на угол α вокруг оси u . Раскрыв скобки, получаем:

${\displaystyle {\begin{array}{lll}\mathbf {v} '&=&\mathbf {v} \cos ^{2}{\frac {\alpha }{2}}+(\mathbf {uv} -\mathbf {vu} )\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-\mathbf {uvu} \sin ^{2}{\frac {\alpha }{2}}\\&=&\mathbf {v} \cos ^{2}{\frac {\alpha }{2}}+2(\mathbf {u} \times \mathbf {v} )\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-(\mathbf {v} (\mathbf {u} \cdot \mathbf {u} )-2\mathbf {u} (\mathbf {u} \cdot \mathbf {v} ))\sin ^{2}{\frac {\alpha }{2}}\\&=&\mathbf {v} (\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}})+(\mathbf {u} \times \mathbf {v} )(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}})+\mathbf {u} (\mathbf {u} \cdot \mathbf {v} )(2\sin ^{2}{\frac {\alpha }{2}})\\&=&\mathbf {v} \cos \alpha +(\mathbf {u} \times \mathbf {v} )\sin \alpha +\mathbf {u} (\mathbf {u} \cdot \mathbf {v} )(1-\cos \alpha )\\&=&(\mathbf {v} -\mathbf {u} (\mathbf {u} \cdot \mathbf {v} ))\cos \alpha +(\mathbf {u} \times \mathbf {v} )\sin \alpha +\mathbf {u} (\mathbf {u} \cdot \mathbf {v} )\\&=&\mathbf {v} _{\bot }\cos \alpha +(\mathbf {u} \times \mathbf {v} _{\bot })\sin \alpha +\mathbf {v} _{\|}\end{array}}}$

где ${\displaystyle \mathbf {v} _{\bot }}$ и ${\displaystyle \mathbf {v} _{\|}}$ — это компоненты вектора v , которые перпендикулярны и параллельны оси u , соответственно.

Получившийся результат является формулой вращения на угол α вокруг оси u .

Умножение вектора на −1 , то есть взятие противоположного кватерниона, не изменяет вращение. В частности, кватернионы 1 и −1 оба определяют тождественное вращение. Более абстрактно, векторы принадлежат группе Ли SU(2) , диффеоморфной 3-сфере. Эта группа двукратно накрывает пространство вращений SO(3).

Вращение четырёхмерного евклидова пространства

Четырёхмерное вращение описывается двумя кватернионами единичной нормы, с точностью до умножения обоих одновременно на −1.

Вариации и обобщения

Похожие формулы позволяют применить бикватернионы для описания преобразований Лоренца — «вращений» 4-мерного пространства Минковского .

См. также

• Карданов подвес

Примечания

Литература

• В. И. Арнольд. . — М. : МЦНМО , 2002. — 40 с. — ISBN 5-94057-025-9 .
• И. Л. Кантор, А. С. Солодовников (недоступная ссылка) . — М.: Наука , 1973. — 144 с.

Ссылки

• от 25 февраля 2009 на Wayback Machine
• от 27 сентября 2007 на Wayback Machine
• от 30 декабря 2013 на Wayback Machine
• от 19 апреля 2014 на Wayback Machine
• // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт . — М. : Советская энциклопедия , 1926—1947.