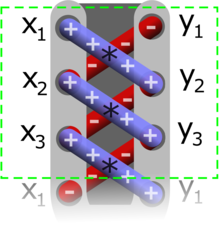
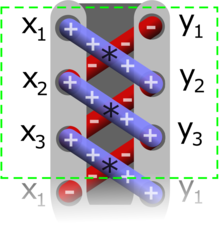
Фо́рмула пло́щади Га́усса ( формула землемера , или формула шнурования , или алгоритм шнурования ) — формула определения площади простого многоугольника , вершины которого заданы декартовыми координатами на плоскости. В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии , лесном хозяйстве и других областях.

Формула была описана (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина .

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самопересекающегося многоугольника, который может быть выпуклым или вогнутым.

Определение

Формула может быть представлена следующим выражением:

${\displaystyle {\begin{aligned}\mathbf {S} &={\frac {1}{2}}\left|\sum _{i=1}^{n-1}x_{i}y_{i+1}+x_{n}y_{1}-\sum _{i=1}^{n-1}x_{i+1}y_{i}-x_{1}y_{n}\right|=\\&={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+\dots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-\dots -x_{n}y_{n-1}-x_{1}y_{n}|,\end{aligned}}}$

где

S — площадь многоугольника,

n — количество сторон многоугольника,

( x _i , y _i ) , i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы :

${\displaystyle {\begin{aligned}\mathbf {S} &={\frac {1}{2}}\left|\sum _{i=1}^{n}x_{i}(y_{i+1}-y_{i-1})\right|=\\&={\frac {1}{2}}\left|\sum _{i=1}^{n}y_{i}(x_{i+1}-x_{i-1})\right|=\\&={\frac {1}{2}}\left|\sum _{i=1}^{n}x_{i}y_{i+1}-x_{i+1}y_{i}\right|=\\&={\frac {1}{2}}\left|\sum _{i=1}^{n}\det {\begin{pmatrix}x_{i}&y_{i}\\x_{i+1}&y_{i+1}\end{pmatrix}}\right|,\end{aligned}}}$

где

x _{n +1} = x ₁ , x ₀ = x _n ,

y _{n +1} = y ₁ , y ₀ = y _n .

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Примеры

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле :

${\displaystyle \mathbf {S} _{\text{tri.}}={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|,}$

где x _i и y _i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3 . По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x ₅ и y ₅ :

${\displaystyle \mathbf {S} _{\text{pent.}}={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|.}$

S для четырехугольника — переменные до x ₄ и y ₄ :

${\displaystyle \mathbf {S} _{\text{quad.}}={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{1}y_{4}|.}$

Более сложный пример

Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

${\displaystyle {\begin{aligned}\mathbf {S} &={\frac {1}{2}}|3\times 11+5\times 8+12\times 5+9\times 6+5\times 4-{}\\&\qquad -4\times 5-11\times 12-8\times 9-5\times 5-6\times 3|=\\&={\frac {60}{2}}=30.\end{aligned}}}$

Объяснение названия

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу . В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

${\displaystyle {\begin{bmatrix}2&4\\3&-8\\1&2\\2&4\end{bmatrix}}.}$

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

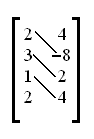
и перемножим пары чисел, соединённых чертой, а затем сложим все произведения:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

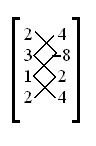
Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь. Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы. В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Хорошее описание «Шнуровки Гаусса» представлено в видео на канале Wild Mathing

См. также

• Планиметр
• Теорема Грина

Примечания