Interested Article - Треугольный паркет
aoibhe
- 2021-02-01
- 1
| Треугольная мозаика | |
|---|---|
|
|
| Тип | Правильная мозаика |
| Вершинная фигура | 3.3.3.3.3.3 (3 6 ) |
| Символ Шлефли | {3,6} |
|
6 | 3 2
3 | 3 3 | 3 3 3 |
|
| Диаграмма Коксетера |
=
|
| Группа симметрии | , [6,3], (*632) |
| Вращательная симметрия |
, [6,3]
+
, (632)
p3 , [3 [3] ] + , (333) |
|
Двойственная
мозаика |
Шестиугольная мозаика |
| Свойства |
Вершинно транзитивна
,
, |
Треуго́льный парке́т ( треугольный паркета́ж ) или треугольная мозаика — это замощение плоскости равными правильными треугольниками , расположенными сторона к стороне.
Треугольная мозаика является двойственной шестиугольной мозаике — если соединить центры смежных треугольников, то проведённые отрезки дадут шестиугольную мозаику . Символ Шлефли треугольного паркета — {3,6}, что означает, что в каждой вершине паркета сходятся 6 треугольников.
Внутренний угол правильного треугольника равен 60 градусов, так что шесть треугольника в одной вершине дают вместе 360 градусов. Это одна из трёх правильных мозаик плоскости . Другие две мозаики — шестиугольный паркет и квадратный паркет .
Английский математик Конвей называл мозаику deltille (дельта-мозаикой), поскольку она имеет форму греческой буквы дельта (Δ). Треугольную мозаику можно также назвать кис-шестиугольной мозаикой, если применить операцию , которая добавляет центральную вершину и треугольники, разбивая грани шестиугольной мозаики .
Однородные раскраски
Существует 9 различных однородных раскрасок треугольной мозаики (по цветам 6 треугольников вокруг вершины — 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314). Три из них можно получить их других путём замены цветов — 111212 и 111112 из 121213, комбинируя 1 и 3, в то время как 111213 получается из 121314 .
Существует один класс , 111112, (помечен *), в котором раскраска не является 1-однородной и содержит перемежающиеся ряды треугольников, в которых каждый третий выкрашен. Приведённая раскраска является 2-однородной и таких имеется бесконечно много, поскольку такие раскраски определяются произвольными сдвигами строк.
| 111111 | 121212 | 111222 | 112122 | 111112(*) |
|
|
|
|
|
| p6m (*632) | p3m1 (*333) | cmm (2*22) | p2 (2222) | p2 (2222) |
| 121213 | 111212 | 111112 | 121314 | 111213 |
|
|
|
|
|
| p31m (3*3) | p3 (333) | |||
Решётка A2 и упаковка кругов
2 как три треугольные мозаики:
+
+
треугольной мозаики называется решёткой A 2 . Она является 2-мерным вариантом .
Решётка A
*
2
(которая также называется A
3
2
) может быть построена как объединение трёх решёток A
2
и эквивалентна решётке A
2
.
-
+
+
= dual of
=
Вершины треугольной мозаики являются центрами наиболее плотной упаковки кругов . Любой круг соприкасается с 6 другими кругами ( контактное число ). Плотность упаковки равна , это около 90,69 %. Поскольку объединение трёх решёток A 2 снова будет решёткой A 2 , круги можно раскрасить в три цвета.
Ячейкой диаграммы Вороного треугольной мозаики является шестиугольник , так что мозаика Вороного , шестиугольная мозаика, имеет прямое отношение к упаковке кругов.
| Решётка A 2 упаковки кругов |
Решётка A
*
2 упаковки кругов |
|---|---|
|
|
Геометрические варианты
Треугольные мозаики могут быть идентичны {3,6} топологии правильной мозаики (6 треугольника в каждой вершине). Существует 5 вершинно транзитивных вариантов с одинаковыми гранями ( ). С точки зрения симметрии все грани имеют одинаковый цвет, раскраска же на рисунках представляет положение в сетке .
-
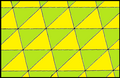Разносторонний треугольник
симметрия p2 -
Разносторонний треугольник
симметрия pmg -
Равнобедренный треугольник
симметрия cmm -
Прямоугольный треугольник
симметрия cmm -
Правильный треугольник
симметрия p6m
Связанные многогранники и мозаики
Плоские мозаики связаны с многогранниками . Располагая меньше треугольников в каждой вершине, получим незаполненное пространство, что позволяет согнуть в фигуру в пирамиду . Отсюда можно получить правильные многогранники : пять, четыре и три треугольника в вершине дают икосаэдр , октаэдр и тетраэдр соответственно.
Эта мозаика топологически связана (как часть последовательности) с правильными многогранниками с символами Шлефли {3,n}.
| Сферическая | Евклидова | Компактная гипербол. |
Пара-
компактная |
Некомпактная гиперболическая | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
| 3.3 | 3 3 | 3 4 | 3 5 | 3 12i | 3 9i | 3 6i | 3 3i | ||||
Эта мозаика топологически связана (как часть последовательности) с полуправильными многогранниками с конфигурацией граней Vn.6.6.
V3.6.6 |
V4.6.6 |
V5.6.6 |
V6.6.6 |
|
Построение Витхоффа из шестиугольных и треугольных мозаик
Подобно однородным многогранникам существует восемь однородных мозаик , базирующихся на правильных шестиугольных мозаиках (или на двойственных треугольных мозаиках).
Если нарисовать плитки исходных граней красным, исходные вершины (получившиеся на их месте многоугольники) жёлтым, а исходные рёбра (получившиеся на их месте многоугольники) синим, существует 8 форм, 7 из которых топологически различны. ( Усечённая треугольная мозаика топологически идентична шестиугольной мозаике.)
| Однородные шестиугольные/треугольные мозаики | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Фундаментальные
домены |
Симметрия : [6,3], (*632) | [6,3] + , (632) | ||||||
| {6,3} | r{6,3} | t{3,6} | sr{6,3} | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Конфиг. | 6 3 | 3.12.12 | (6.3) 2 | 6.6.6 | 3 6 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 |
| Треугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 3 3 | 3 3 | 3 | 3 | 3 3 | 3 3 | 3 | 3 | 3 3 | 3 3 | 3 | 3 3 3 | | | 3 3 3 | ||||
| Коксетер |
|
|
|
|
|
|
|
|
|||
|
Рисунок
Вершинная фигура |
|
3.6.3.6 |
|
3.6.3.6 |
|
3.6.3.6 |
6.6.6 |
|
|||
Связанные правильные комплексные бесконечноугольники
Существует 4 , имеющих те же вершины шестиугольной мозаики. Рёбра правильных комплексных апейрогонов могут содержать 2 и более вершин. Правильные апейрогоны p { q } r имеют ограничение: 1/ p + 2/ q + 1/ r = 1. Рёбра имеют p вершин и вершинные фигуры являются r - угольниками .
Первый апейрогон состоит из 2-рёбер, следующие два имеют треугольные рёбра, последний имеет перекрывающиеся шестиугольные рёбра.
|
|
|
|
2{6}6 или
|
3{4}6 или
|
3{6}3 или
|
6{3}6 или
|
|---|
Другие треугольные мозаики
Существуют также три , состоящие из треугольников одного типа:
30°-60°-90° прямоугольные треугольники |
Разделённая квадратная 45°-45°-90° прямоугольные треугольники |
30°-30°-120° равнобедренные треугольники |
См. также
- Замощение
- Полиамонд
- Шестиугольная решётка
- Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
- (структурное проектирование, использующее треугольную мозаику)
Примечания
- ↑ , с. 147.
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- , с. 102-107.
- . Дата обращения: 26 марта 2017. 25 февраля 2021 года.
- , с. 74–75, pattern 1.
- , с. 473-481.
- , с. 111-112, 136.
Литература
- С.В. Голомб. = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М. : Мир, 1975. — С. 147. — 207 с.
- B. Grünbaum , G.C. Shephard. Chapter 2.1: Regular and uniform tilings , Chapter 2.9 Archimedean and Uniform colorings // . — New York: W. H. Freeman & Co., 1987. — С. —65,102—107. — ISBN 0-7167-1193-1 .
- R. Williams. . — New York: Dover Publications , 1979. — С. . — ISBN 0-486-23729-X .
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strass. . — 2008. — ISBN 978-1-56881-220-5 . от 19 сентября 2010 на Wayback Machine
- H. S. M. Coxeter . Regular Complex Polytopes. — 2ed. — New York, Port Chester, Melbourne, Sydney: Cambridge University Press, 1991. — ISBN 0-521-39490-2 .
- Keith Critchlow. Order in Space: A design source book. — New York: Thames & Hudson, 1987. — ISBN 0-500-34033-1 .
Ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- Klitzing, Richard.
- Amit Patel. . — Алгоритмы представления шестиугольной и треугольной сеток в компьютерных стратегических играх.
|
Фундаментальные выпуклые
и
соты в пространствах размерности 2–10
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Периодичные | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Апериодичные | |||||||||
| Другие | |||||||||
|
По
вершинной
конфигурации |
|
||||||||
aoibhe
- 2021-02-01
- 1
