Уравне́ние состоя́ния — соотношение, отражающее для конкретного класса термодинамических систем связь между характеризующими её макроскопическими физическими величинами , такими как температура , давление , объём , химический потенциал , энтропия , внутренняя энергия , энтальпия и др. Уравнения состояния необходимы для получения с помощью математического аппарата термодинамики конкретных результатов, касающихся рассматриваемой системы . Эти уравнения не содержатся в постулатах термодинамики, так что для каждого выбранного для изучения макроскопического объекта их либо определяют эмпирически, либо для модели изучаемой системы находят методами статистической физики . В рамках термодинамики уравнения состояния считают заданными при определении системы . Если изучаемый объект допускает термодинамическое описание, то это описание выполняют посредством уравнений состояния, которые для реальных веществ могут иметь весьма сложный вид.

О терминологии

Из множества уравнений состояния выделяются:

• уравнения состояния, выражающие интенсивные переменные состояния , входящие в фундаментальное уравнение Гиббса в энергетическом выражении и фундаментальное уравнение Гиббса энтропийном выражении , в виде функций от экстенсивных переменных состояния — аргументов соответствующего фундаментального уравнения Гиббса (см. примечание );
• термические уравнения состояния , выражающие связь между температурой, обобщёнными термодинамическими координатами (к которым в данном случае причислены количества составляющих систему веществ ) и обобщёнными термодинамическими силами (к которым в данном случае причислены химические потенциалы составляющих систему веществ ) . Обычно под уравнениями состояния, если специально не оговаривается, подразумевают термические уравнения состояния . Величины, входящие термическое уравнение состояния, именуют первичными термическими величинам ;
• калорические уравнения состояния , отражающие связь между первичными калорическими величинами и первичными термическими величинами. В качестве первичных калорических величин обычно выступают термодинамические потенциалы (чаще всего внутренняя энергия и энтальпия ) и энтропия как родоначальница ряда функций Массье — Планка ;
• канонические уравнения состояния (фундаментальные уравнения Гиббса для термодинамических потенциалов), представляющие собой выражения для термодинамических потенциалов как функций их естественных независимых переменных .

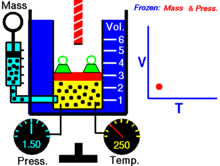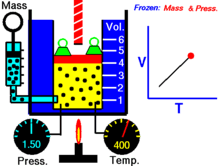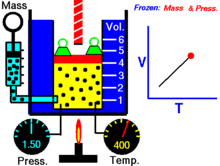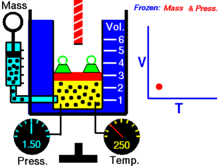
В русскоязычной учебной литературе получила распространение более узкая трактовка понятий «термические уравнения состояния» и «калорическое уравнение состояния», позволяющая за счёт потери общности заметно упростить изложение рассматриваемого вопроса. А именно, в узком смысле под термическим уравнением состояния понимают зависимость обобщённой силы ${\displaystyle X_{i}}$ или химического потенциала ${\displaystyle \mu _{j}}$ от температуры ${\displaystyle T}$ , обобщённых координат ${\displaystyle x_{i}}$ и масс составляющих веществ ${\displaystyle m_{j}}$ :

${\displaystyle X_{i}=X_{i}(T,\{x_{i}\},\{m_{j}\}),}$

(выражение ${\displaystyle \{x_{i}\}}$ есть сокращение для перечисления ${\displaystyle x_{1},x_{2},...,x_{i},...}$ переменных определённого типа, в данном случае — обобщённых координат). В узком смысле под калорическим уравнением состояния понимают зависимость от температуры и других первичных термических величин внутренней энергии ${\displaystyle U}$ :

${\displaystyle U=U(T,\{x_{i}\},\{m_{j}\}),}$

или энтальпии ${\displaystyle H}$ .

Общее число уравнений состояния (все термические плюс калорическое) термодинамической системы при таком подходе равно числу термодинамических степеней свободы системы, то есть числу независимых переменных, характеризующих состояние системы, а их полный набор необходим и достаточен для исчерпывающего описания термодинамических свойств системы .

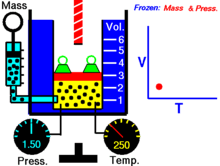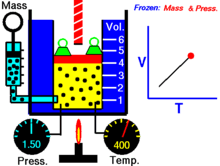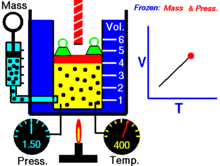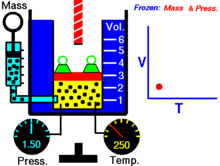
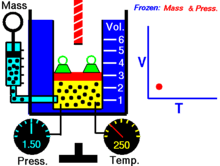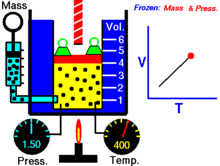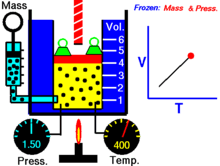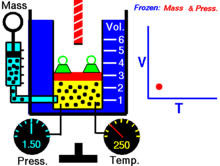
Далее — если иное не оговорено особо — для большей наглядности речь будет идти об однородных закрытых термодеформационных системах в статическом (локальноравновесном) состоянии . Вариантность такой системы равна двум (см. Правило Дюгема ) и для её полного описания — помимо калорического уравнения состояния — требуется единственное термическое уравнение состояния. Простейшим примером такой системы служит газ в цилиндре с поршнем.

Термическое уравнение состояния

Термическое уравнение состояния (ТУС, термин введён Х. Камерлинг-Оннесом ) для закрытой термодеформационной системы связывает между собой её давление, объём и температуру; его общий вид можно записать так :

${\displaystyle f(P,\;V,\;T)=0.}$

(Термическое уравнение состояния, заданное как неявная функция)

Или же так:

${\displaystyle f(P,\;V,\;T)=1.}$

(Термическое уравнение состояния, заданное как иная неявная функция)

Таким образом, чтобы задать термическое уравнение состояния необходимо конкретизировать вид функции ${\displaystyle f}$ .

Для идеального газа (как классического, так и квазиклассического) его термическое уравнение состояния известно как уравнение Клапейрона (уравнение Клапейрона — Менделеева) :

${\displaystyle PV={\frac {m}{M}}RT,}$

где ${\displaystyle R}$ — универсальная газовая постоянная , ${\displaystyle m}$ — масса газа, ${\displaystyle M}$ — его молярная масса .

Для фотонного газа его давление зависит только от температуры, а термическое уравнение состояния выглядит так :

${\displaystyle P={\frac {a}{3}}T^{4},}$

(Термическое уравнение состояния фотонного газа)

где a — радиационная постоянная .

Для макроскопических объектов, требующих от термодинамики учёта их магнитных и электрических свойств, термические уравнения состояния имеют следующий вид :

${\displaystyle {\vec {M}}={\vec {M}}(T,{\vec {H}}),}$

(Термическое уравнение состояния магнетика)

${\displaystyle {\vec {P}}={\vec {P}}(T,{\vec {E}}),}$

(Термическое уравнение состояния электрически поляризуемой среды)

где ${\displaystyle {\vec {M}}}$ — намагниченность вещества, ${\displaystyle {\vec {H}}}$ — напряжённость магнитного поля , ${\displaystyle {\vec {P}}}$ — поляризованность вещества, ${\displaystyle {\vec {E}}}$ — напряжённость электрического поля .

Для упругого стержня (из изотропного материала) длиной L , на который действует сила F , направленная вдоль стержня, термическое уравнение состояния выглядит так :

${\displaystyle L=L(T,F).}$

(Термическое уравнение состояния упругого стержня)

Термические коэффициенты

Выражая одну из переменных в через две другие, для простой закрытой системы в зависимости от выбора независимых переменных термическое уравнение состояния можно записать тремя способами :

${\displaystyle P=P(T,V),}$

(Термическое уравнение состояния с независимыми переменными T и V )

${\displaystyle V=V(T,P),}$

(Термическое уравнение состояния с независимыми переменными T и P )

${\displaystyle T=T(V,P).}$

(Термическое уравнение состояния с независимыми переменными V и P )

Запишем эти уравнения в дифференциальной форме :

${\displaystyle dP=\left({\frac {\partial P}{\partial T}}\right)_{V}dT+\left({\frac {\partial P}{\partial V}}\right)_{T}dV,}$

(Дифференциальное ТУС с независимыми переменными T и V )

${\displaystyle dV=\left({\frac {\partial V}{\partial T}}\right)_{P}dT+\left({\frac {\partial V}{\partial P}}\right)_{T}dP,}$

(Дифференциальное ТУС с независимыми переменными T и P )

${\displaystyle dT=\left({\frac {\partial T}{\partial P}}\right)_{V}dP+\left({\frac {\partial T}{\partial V}}\right)_{P}dV.}$

(Дифференциальное ТУС с независимыми переменными P и V )

В приведённые уравнения входят шесть частных производных, которые попарно обратны друг другу:

${\displaystyle \left({\frac {\partial T}{\partial P}}\right)_{V}=\left[\left({\frac {\partial P}{\partial T}}\right)_{V}\right]^{-1},}$ ${\displaystyle \left({\frac {\partial T}{\partial V}}\right)_{P}=\left[\left({\frac {\partial V}{\partial T}}\right)_{P}\right]^{-1},}$ ${\displaystyle \left({\frac {\partial P}{\partial V}}\right)_{T}=\left[\left({\frac {\partial V}{\partial P}}\right)_{T}\right]^{-1},}$

поэтому самостоятельное значение имеют только три из них. В качестве основных обычно выбирают производные

${\displaystyle \left({\frac {\partial V}{\partial T}}\right)_{P},}$ ${\displaystyle \left({\frac {\partial V}{\partial P}}\right)_{T}}$ и ${\displaystyle \left({\frac {\partial P}{\partial T}}\right)_{V},}$

которые называют термическими коэффициентами . Название отражает связь этих коэффициентов с термическим уравнением состояния.

Из математического анализа известно, что для любой неявно заданной функции трёх переменных

${\displaystyle f(P,\;V,\;T)=0}$

справедливо соотношение

${\displaystyle \left({\frac {\partial P}{\partial T}}\right)_{V}\left({\frac {\partial T}{\partial V}}\right)_{P}\left({\frac {\partial V}{\partial P}}\right)_{T}=-1,}$

(Термическое уравнение состояния в дифференциальной форме)

или

${\displaystyle \left({\frac {\partial P}{\partial V}}\right)_{T}\left({\frac {\partial V}{\partial T}}\right)_{P}\left({\frac {\partial T}{\partial P}}\right)_{V}=-1,}$

то есть любой из трёх термических коэффициентов можно выразить через два других. Это соотношение иногда называют термическим уравнением состояния в дифференциальной форме .

На практике используют не сами частные производные, а образованные из них коэффициенты (также называемые термическими коэффициентами , либо же термодинамическими коэффициентами ):

изобарный коэффициент термического расширения

${\displaystyle \alpha \equiv {\frac {1}{V}}\left({\frac {\partial V}{\partial T}}\right)_{P},}$

(Изобарный коэффициент объёмного расширения; коэффициент термического расширения; температурный коэффициент всестороннего расширения; термический коэффициент всестороннего расширения)

характеризующий скорость изменения объёма при изменении температуры в условиях постоянного давления (для идеального газа ${\displaystyle \alpha =1/T}$ );

термический коэффициент давления при постоянном объёме

${\displaystyle \beta \equiv {\frac {1}{P}}\left({\frac {\partial P}{\partial T}}\right)_{V},}$

(Изохорный коэффициент давления; температурный коэффициент давления; термический коэффициент давления; коэффициент термической упругости)

характеризующий скорость изменения давления при изменении температуры в условиях постоянного объёма (для идеального газа ${\displaystyle \beta =1/T}$ );

изотермический коэффициент всестороннего сжатия

${\displaystyle \chi \equiv -{\frac {1}{V}}\left({\frac {\partial V}{\partial P}}\right)_{T},}$

(Изотермический коэффициент всестороннего сжатия; коэффициент изотермического сжатия; коэффициент объёмного сжатия; коэффициент сжимаемости; коэффициент объёмной упругости; коэффициент объёмного упругого расширения)

характеризующий скорость изменения объёма при изменении давления в условиях постоянной температуры (для идеального газа ${\displaystyle \chi =1/P}$ ). Знак минус указывает на уменьшение объёма с повышением давления и нужен для того, чтобы избежать отрицательных значений коэффициента сжимаемости .

Из вытекает уравнение связи между коэффициентами объёмного расширения, упругости и сжатия :

${\displaystyle \beta ={\frac {\alpha }{\chi P}}.}$

(Уравнение связи между коэффициентами объёмного расширения, упругости и сжатия)

Это соотношение позволяет, например, найти коэффициент ${\displaystyle \beta }$ для твёрдых и жидких тел (которые практически невозможно нагреть или охладить без изменения их объёма) по определяемым опытным путём коэффициентам ${\displaystyle \alpha }$ и ${\displaystyle \chi }$ .

Термические коэффициенты являются функциями объёма, давления и температуры. Практическое значение коэффициентов объёмного расширения, упругости и сжатия состоит в том, что они используются для вычисления тех термодинамических величин, которые затруднительно или невозможно определить экспериментально.

Калорическое уравнение состояния

Если в в качестве обязательной переменной (зависимой или независимой) входит температура, то калорическое уравнение состояния (КУС) для простой закрытой системы отражает зависимость внутренней энергии от термодинамических параметров состояния (температуры и объёма, температуры и давления, объёма и давления) (авторство термина КУС принадлежит Х. Камерлинг-Оннесу ) :

${\displaystyle U=U(T,V),}$

(Калорическое уравнение состояния с независимыми переменными T и V )

${\displaystyle U=U(T,P),}$

(Калорическое уравнение состояния с независимыми переменными T и P )

${\displaystyle U=U(V,P).}$

(Калорическое уравнение состояния с независимыми переменными V и P )

Калорические коэффициенты

Калорические коэффициенты вводят способом, аналогичным способу введения термических коэффициентов. Запишем с независимыми переменными ${\displaystyle T}$ и ${\displaystyle V}$ в дифференциальной форме :

${\displaystyle dU=\left({\frac {\partial U}{\partial T}}\right)_{V}dT+\left({\frac {\partial U}{\partial V}}\right)_{T}dV,}$

(Дифференциальное КУС с независимыми переменными ${\displaystyle T}$ и ${\displaystyle V}$ )

и посредством входящих в это соотношение частных производных введём первую пару калорических коэффициентов — теплоёмкость при постоянном объёме

${\displaystyle C_{V}\equiv \left({\frac {\partial U}{\partial T}}\right)_{V}}$

(Теплоёмкость при постоянном объёме)

и теплоту изотермического расширения

${\displaystyle l\equiv \left({\frac {\partial U}{\partial V}}\right)_{T}+P,}$

(Теплота изотермического расширения)

имеющую размерность давления. Применявшееся ранее для этого калорического коэффициента название скрытая теплота расширения как пережиток теории теплорода к использованию не рекомендуется .

Для идеального газа теплоёмкость при постоянном объёме ${\displaystyle C_{V}}$ равна : ${\displaystyle {\frac {3Rm}{2M}}}$ для одноатомных, ${\displaystyle {\frac {5Rm}{2M}}}$ для двухатомных и ${\displaystyle {\frac {3Rm}{M}}}$ для многоатомных газов. Здесь ${\displaystyle m}$ — масса газа, ${\displaystyle M}$ — молярная масса этого газа, ${\displaystyle R}$ — универсальная газовая постоянная . Теплота изотермического расширения идеального газа ${\displaystyle l=P}$ .

Частная производная

${\displaystyle P_{int}\equiv \left({\frac {\partial U}{\partial V}}\right)_{T}=l-P}$

(Внутреннее давление)

носит название внутреннего давления и к калорическим коэффициентам не относится, хотя и вводится одновременно с ними. Численное значение этой величины (отражающей на молекулярном уровне взаимное притяжение частиц), мало для реальных газов и очень велико (по сравнению с обычными значениями внешнего давления) для жидкостей и твёрдых тел . Для идеального газа ${\displaystyle P_{int}=0,}$ то есть внутренняя энергия идеального газа не зависит от объёма (закон Джоуля ) .

Введём вторую пару калорических коэффициентов, связанных с с независимыми переменными ${\displaystyle T}$ и ${\displaystyle P}$ — теплоёмкость при постоянном давлении

${\displaystyle C_{P}\equiv \left({\frac {\partial U}{\partial T}}\right)_{P}+P\left({\frac {\partial V}{\partial T}}\right)_{P}}$

(Теплоёмкость при постоянном давлении, выраженная через внутреннюю энергию)

и теплоту изотермического возрастания давления

${\displaystyle h\equiv \left({\frac {\partial U}{\partial P}}\right)_{T}+P\left({\frac {\partial V}{\partial P}}\right)_{T}.}$

(Теплота изотермического возрастания давления, выраженная через внутреннюю энергию)

В литературе эти калорические коэффициенты чаще приводят в более компактном и удобном для расчётов виде, используя энтальпию ${\displaystyle H\equiv U+PV}$ или энтропию ${\displaystyle S}$ :

${\displaystyle C_{P}=\left({\frac {\partial H}{\partial T}}\right)_{P}=T\left({\frac {\partial S}{\partial T}}\right)_{P},}$

(Теплоёмкость при постоянном давлении, выраженная через энтальпию)

${\displaystyle h=\left({\frac {\partial H}{\partial P}}\right)_{T}-V=T\left({\frac {\partial S}{\partial P}}\right)_{T}.}$

(Теплота изотермического возрастания давления; теплота изотермического сжатия)

Для идеального газа ${\displaystyle C_{P}}$ и ${\displaystyle C_{V}}$ связаны . Коэффициент ${\displaystyle h}$ в подавляющем большинстве случаев есть величина отрицательная; для идеального газа ${\displaystyle h=-V}$ . Применявшееся ранее для этого калорического коэффициента название скрытая теплота изменения давления к использованию не рекомендуется.

Приведём определения для последней пары калорических коэффициентов, связанных с с независимыми переменными ${\displaystyle V}$ и ${\displaystyle P}$ — теплоты изохорного сжатия

${\displaystyle \varkappa \equiv \left({\frac {\partial U}{\partial P}}\right)_{V}}$

(Теплота изохорного сжатия)

и теплоты изобарного расширения

${\displaystyle \lambda \equiv \left({\frac {\partial U}{\partial V}}\right)_{P}+P.}$

(Теплота изобарного расширения)

Четыре из шести введённых калорических коэффициентов ( ${\displaystyle C_{P},C_{V},}$ ${\displaystyle l}$ и ${\displaystyle h}$ ), имея самостоятельный физический смысл, являются полезными вспомогательными величинами при выводе термодинамических соотношений и в термодинамических расчётах, в частности, при вычислении внутренней энергии, энтальпии и энтропии. Коэффициенты ${\displaystyle \varkappa }$ и ${\displaystyle \lambda }$ в настоящее время вышли из употребления .

Связь между термическими и калорическими коэффициентами

Полезные соотношения, связывающие термические и калорические коэффициенты :

${\displaystyle P_{int}=\left({\frac {\partial U}{\partial V}}\right)_{T}=T\left({\frac {\partial P}{\partial T}}\right)_{V}-P={\frac {\alpha }{\chi }}T-P,}$

(Уравнение связи между термическим и калорическим уравнениями состояния)

${\displaystyle h=l\left({\frac {\partial V}{\partial T}}\right)_{P}=-T\left({\frac {\partial V}{\partial T}}\right)_{P}=-\alpha TV,}$

${\displaystyle C_{P}=C_{V}+l\left({\frac {\partial V}{\partial T}}\right)_{P}=C_{V}+\alpha lV=C_{V}+{\frac {{\alpha }^{2}}{\chi }}TV,}$

${\displaystyle {\frac {C_{P}}{C_{V}}}={\frac {\left({\frac {\partial P}{\partial V}}\right)_{S}}{\left({\frac {\partial P}{\partial V}}\right)_{T}}}.}$

(Теорема Реша, 1854 )

Для идеального газа

${\displaystyle C_{P}=C_{V}+{\frac {mR}{M}}.}$

(Формула Майера )

Каноническое уравнение состояния

Основная статья: Термодинамические потенциалы .

Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов ( внутренней энергии , энтальпии , свободной энергии или потенциала Гиббса ) через независимые переменные, относительно которых записывается его полный дифференциал.

• ${\displaystyle U=U(S,\;V)}$ (для внутренней энергии),
• ${\displaystyle H=H(S,\;P)}$ (для энтальпии),
• ${\displaystyle F=F(T,\;V)}$ (для энергии Гельмгольца),
• ${\displaystyle G=G(T,\;P)}$ (для потенциала Гиббса).

Каноническое уравнение, независимо от того, в каком из этих четырёх видов оно представлено, содержит полную информацию о термических и калорических свойствах термодинамической системы (предполагается, что известно и определение термодинамического потенциала, такое, как F = U − TS ).

Уравнения состояния газов

К уравнениям состояния газов относятся:

• Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона)
• Уравнение Ван-дер-Ваальса (уравнение состояния реального газа)
• Уравнение Дитеричи
• Уравнение состояния Редлиха — Квонга
• Уравнение состояния Барнера — Адлера
• Уравнение состояния Суги — Лю
• Уравнение состояния Ли — Эрбара — Эдмистера

Уравнения состояния жидкостей

• Уравнение состояния Бенедикта — Вебба — Рубина
• Модели локального состава ( Модель Вильсона , NRTL , , , )

Уравнения состояния твёрдых тел

Состояние твёрдых тел можно описать с помощью уравнения Ми — Грюнайзена

См. также

• Термодинамическое равновесие
• Закон соответственных состояний

Примечания

Литература

• Münster A. Classical Thermodynamics. — London e. a.: Wiley-Interscience, 1970. — xiv + 387 p. — ISBN 0 471 62430 6 .
• Александров А. А. Термодинамические основы циклов теплоэнергетических установок. — М. : Издательский дом МЭИ, 2016. — 159 с. — ISBN 978-5-383-00961-1 .
• Базаров И. П. Заблуждения и ошибки в термодинамике. — 2-е изд., испр. — М. : Едиториал УРСС, 2003. — 120 с. — ISBN 5-354-00391-1 .
• Базаров И. П. (недоступная ссылка) . — М.: Высшая школа, 1991. — 376 с.
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.— Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3 .
• Барилович B. A., Смирнов Ю. А. Основы технической термодинамики и теории тепло- и массообмена. — М. : ИНФРА-М, 2014. — 432 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-005771-2 .
• Бахшиева Л. Т. и др. Техническая термодинамика и теплотехника / Под ред. проф А. А. Захаровой. — 2-е изд., испр. — М. : Академия, 2008. — 272 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-4999-1 .
• Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М. : Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0 .
• Белоконь Н. И. Основные принципы термодинамики. — М. : Недра, 1968. — 112 с.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 1. Основной курс. — М. : Дрофа, 2009. — 480 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06031-9 .
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М. : Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8 .
• Бурсиан В. Р. , Соколов П. Т. Лекции по термодинамике. — Л. : Кубуч, 1934. — 352 с.
• Василевский А. С. Термодинамика и статистическая физика. — 2-е изд., перераб.. — М. : Дрофа, 2006. — 240 с. — ISBN 5-7107-9408-2 .
• Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М. : Химия, 1970. — Т. I. — 592 с.
• Глазов В. М. Основы физической химии. — М. : Высшая школа, 1981. — 456 с.
• Гуйго Э. И., Данилова Г. Н., Филаткин В. Н. и др. Техническая термодинамика / Под общ. ред. проф. Э. И. Гуйго. — Л. : Изд-во Ленингр. ун-та, 1984. — 296 с.
• Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева . — Л.—М.: Госхимиздат, 1941. — 188 с.
• Зубарев Д. Н. (рус.) // Физическая энциклопедия . — Большая Российская энциклопедия , 1998. — Т. 5: Стробоскопические приборы — Яркость . — С. 236 .
• Карапетьянц М. Х. Химическая термодинамика. — М. : Химия, 1975. — 584 с.
• Квасников И. А. Термодинамика и статистическая физика. Т. 1: Теория равновесных систем: Термодинамика. — 2-е изд., сущ. перераб. и доп. — М. : Едиториал УРСС, 2002. — 240 с. — ISBN 5-354-00077-7 .
• Коган В. Е., Литвинова Т. Е., Чиркст Д. Э., Шахпаронова Т. С. Физическая химия / Науч. ред. проф. Д. Э. Чиркст. — СПб. : Национальный минерально-сырьевой ун-т «Горный», 2013. — 450 с.
• Колесников И. М. Термодинамика физико-химических процессов. — М. : Гос. акад. нефти и газа им. И. М. Губкина, 1994. — 288 с.
• Колесников И. М. Термодинамика физико-химических процессов. — М. : Нефть и Газ, 2005. — 480 с. — ISBN 5-7246-0351-9 .
• Коновалов В. И. Техническая термодинамика. — Иваново: Иван. гос. энерг. ун-т, 2005. — 620 с. — ISBN 5-89482-360-9 .
• Кубо Р. Термодинамика. — М. : Мир, 1970. — 304 с.
• Кудрявцева И. В., Рыков А. В., Рыков В. А. . — СПб. — Научный журнал НИУ ИТМО.- Статья. — УДК 536.71
• Куранов Г. Л. (рус.) // Химическая энциклопедия . — Большая Российская энциклопедия , 1998. — Т. 5: Триптофан — Ятрохимия . — С. 39—40 .
• Маляренко В. А., Редько А. Ф., Чайка Ю. И., Поволочко В. Б. Техническая теплофизика ограждающих конструкций зданий и сооружений. — Харьков: Рубикон, 2001. — 280 с. — ISBN 966-7152-47-2 .
• Мурзаков В. В. Основы технической термодинамики. — М. : Энергия, 1973. — 304 с.
• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М. : Мир, 1971. — 296 с.
• Николаев Г. П., Лойко А. Э. Техническая термодинамика. — Екатеринбург: УрФУ, 2013. — 227 с.
• Партингтон Дж. Р., Раковский А. В. [libgen.io/book/index.php?md5=7e1f282c5a99198778a5d15a18a6018b Курс химической термодинамики] / Пер. с англ. Я. В. Герасимова, проработка и дополнения проф. А. В. Раковского. — 2-е изд., стереотипное. — М. — Л. : Госхимтехиздат , 1932. — 383 с.
• Полторак О. М. Термодинамика в физической химии. — М. : Высшая школа, 1991. — 320 с. — ISBN 5-06-002041-X .
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М. : Наука, 1971. — 376 с.
• Пыхачев Г. Б., Исаев Р. Г. Подземная гидравлика. — М. : Недра, 1973. — 360 с.
• Рыков С. В., Кудрявцева И. В., Рыков А. В., Курова Л. В. . — СПб. — Научный журнал НИУ ИТМО.- Статья. — УДК 536.71
• Рудой Ю. Г. (рус.) // Большая российская энциклопедия . — Большая Российская энциклопедия (издательство) , 2017. — Т. 33 . — С. 65 .
• Сивухин Д. В. Общий курс физики. Т. II. Термодинамика и молекулярная физика. — 5-е изд., испр. — М. : ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5 .
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М. : Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0 .
• Толпыго К. Б. [www.libgen.io/book/index.php?md5=9D8053F983EF1E982792F381F436A461 Термодинамика и статистическая физика]. — Киев: Изд-во Киевского ун-та, 1966. — 364 с. (недоступная ссылка)
• Щелкачев В. Н., Лапук Б. Б. Подземная гидравлика / Под общ. ред. акад. Л. С. Лейбензона. — М. — Л: Гостоптехиздат, 1949. — 524 с.
• Эпштейн П.С. Курс термодинамики / Пер.с англ. Н. М.Лозинской, Н. А.Толстого.. — ОГИЗ. — М. , 1948. — 420 с.