Пло́тность вероя́тности — один из способов задания распределения случайной величины . Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины » или « функция распределения вероятностей » фактически синонимизируются ^{[ источник не указан 1297 дней ]} и под ними подразумевается вещественная функция , характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Прикладное описание понятия

Плотность распределения одномерной непрерывной случайной величины ${\displaystyle \xi }$ — это числовая функция ${\displaystyle f(x)}$ , отношение ${\displaystyle f(x_{1})/f(x_{2})}$ значений которой в точках ${\displaystyle x_{1}}$ и ${\displaystyle x_{2}}$ задаёт отношение вероятностей попаданий величины ${\displaystyle \xi }$ в узкие интервалы равной ширины ${\displaystyle [x_{1},x_{1}+\Delta x]}$ и ${\displaystyle [x_{2},x_{2}+\Delta x]}$ вблизи данных точек.

Плотность распределения неотрицательна при любом ${\displaystyle x}$ и нормирована, то есть

${\displaystyle \int _{-\infty }^{+\infty }f(x)\,{\mbox{d}}x=1}$

При стремлении ${\displaystyle x}$ к ${\displaystyle \,\pm \infty }$ функция ${\displaystyle f(x)}$ стремится к нулю. Размерность плотности распределения всегда обратная к размерности случайной величины — если ${\displaystyle \xi }$ исчисляется в метрах, то размерностью ${\displaystyle f}$ будет м ^-1 .

Если в конкретной ситуации известно выражение для ${\displaystyle f(x)}$ , с его помощью можно вычислить вероятность попадания величины ${\displaystyle \xi }$ в интервал ${\displaystyle [a,b]}$ как

${\displaystyle P(\xi \in [a,b])=\int _{a}^{b}f(x)\,{\mbox{d}}x}$ .

Зная плотность вероятности, можно также определить наиболее вероятное значение ( моду ) случайной величины как максимум ${\displaystyle f(x)}$ . Также с помощью плотности вероятности находится среднее значение случайной величины:

${\displaystyle E\xi =\int _{-\infty }^{+\infty }xf(x)\,{\mbox{d}}x}$

и среднее значение измеримой функции ${\displaystyle g(\xi )}$ случайной величины:

${\displaystyle \langle g(\xi )\rangle =\int _{-\infty }^{+\infty }g(x)f(x)\,{\mbox{d}}x}$ .

Чтобы перейти к плотности распределения ${\displaystyle {f}_{\chi }(y)}$ другой случайной величины ${\displaystyle \chi =z(\xi )}$ , нужно взять

${\displaystyle {f}_{\chi }(y)=f(z^{-1}(y))\cdot \left|{\frac {{\mbox{d}}z^{-1}(y)}{{\mbox{d}}y}}\right|}$ ,

где ${\displaystyle z^{-1}(y)}$ — обратная функция по отношению к ${\displaystyle y=z(x)}$ (предполагается, что z — взаимно однозначное отображение ).

Значение плотности распределения ${\displaystyle f(x_{1})}$ не является вероятностью принять случайной величиной значение ${\displaystyle x_{1}}$ . Так, вероятность принятия непрерывной случайной величиной ${\displaystyle \xi }$ значения ${\displaystyle x_{1}}$ равна нулю. При непрерывном распределении случайной величины ${\displaystyle \xi }$ вопрос может ставиться о вероятности её попадания в некий диапазон, а не о вероятности реализации её конкретного значения.

Интеграл

${\displaystyle \int _{-\infty }^{x}f(t)\,{\mbox{d}}t=F(x)}$

называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция ${\displaystyle F}$ является неубывающей и изменяется от 0 при ${\displaystyle x\to -\infty }$ до 1 при ${\displaystyle x\to +\infty }$ .

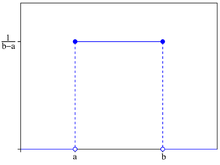
Самым простым распределением является равномерное распределение на отрезке ${\displaystyle [a,b]}$ . Для него плотность вероятности равна:

${\displaystyle f(x)=\left\{{\begin{matrix}{1 \over b-a},&x\in [a,b]\\0,&x\not \in [a,b]\end{matrix}}\right..}$

Широко известным распределением является « нормальное », оно же гауссово, плотность которого записывается как

${\displaystyle f(x)={\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left[-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right]}$ ,

где ${\displaystyle \mu }$ и ${\displaystyle \sigma }$ — параметры: математическое ожидание и среднеквадратичное отклонение . Другие примеры плотностей распределения — одностороннее лапласовское ( ${\displaystyle \lambda >0}$ ):

${\displaystyle f(x)=A\exp \left[-\lambda \,x\right]\,\,(x\geq 0)}$ и ${\displaystyle f(x)=0\,\,(x<0)}$ ,

и максвелловское ( ${\displaystyle \alpha >0}$ ):

${\displaystyle f(x)=Ax^{2}\exp \left[-\alpha x^{2}\right]\,\,(x\geq 0)}$ и ${\displaystyle f(x)=0\,\,(x<0)}$ .

В двух последних примерах множитель ${\displaystyle A}$ подбирается в зависимости от параметра ${\displaystyle \lambda }$ или ${\displaystyle \alpha }$ так, чтобы обеспечить нормировку интеграла от плотности вероятности. В случае распределения Лапласа оказывается, что ${\displaystyle A=\lambda }$ .

Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе . При этом для аргумента функции ${\displaystyle f}$ нередко используют тот же символ, что и для рассматриваемой в физической задаче случайной величины (как если бы выше на месте ${\displaystyle \xi }$ всюду стояло ${\displaystyle x}$ ). Так, в выражении максвелловской плотности распределения пишут не формальную переменную ${\displaystyle x}$ , а символ скорости ${\displaystyle v}$ . В простейших ситуациях такая вольность с обозначениями не приводит к недоразумениям.

Спадающий при стремлении аргумента к ${\displaystyle +\infty }$ или ${\displaystyle -\infty }$ участок графика плотности вероятности ${\displaystyle f(x)}$ в областях, где ${\displaystyle f\ll f_{max}}$ , называется хвостом . Из упомянутых распределений, нормальное и лапласовское имеют по два хвоста (слева и справа), а максвелловское в выписанном виде — один (справа).

Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность ${\displaystyle f}$ нередко является функцией нескольких величин, в рассуждениях неявно предполагались не всегда гарантируемые непрерывность и дифференцируемость функций и так далее.

Определение плотности вероятности в теории меры

Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве ${\displaystyle \mathbb {R} ^{n}}$ . Пусть ${\displaystyle \mathbb {P} }$ является вероятностной мерой на ${\displaystyle \mathbb {R} ^{n}}$ , то есть определено вероятностное пространство ${\displaystyle \left(\mathbb {R} ^{n},{\mathcal {B}}(\mathbb {R} ^{n}),\mathbb {P} \right)}$ , где ${\displaystyle {\mathcal {B}}(\mathbb {R} ^{n})}$ обозначает борелевскую σ-алгебру на ${\displaystyle \mathbb {R} ^{n}}$ . Пусть ${\displaystyle m}$ обозначает меру Лебега на ${\displaystyle \mathbb {R} ^{n}}$ . Вероятность ${\displaystyle \mathbb {P} }$ называется абсолютно непрерывной (относительно меры Лебега) ( ${\displaystyle \mathbb {P} \ll m}$ ), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

${\displaystyle \forall B\in {\mathcal {B}}(\mathbb {R} ^{n}),\;(m(B)=0)\Rightarrow (\mathbb {P} (B)=0).}$

Если вероятность ${\displaystyle \mathbb {P} }$ абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция ${\displaystyle f\colon \mathbb {R} ^{n}\to [0,\infty )}$ такая, что

${\displaystyle \mathbb {P} (B)=\int \limits _{B}f(x)\,dx}$ ,

где использовано общепринятое сокращение ${\displaystyle m(dx)\equiv dx}$ , и интеграл понимается в смысле Лебега .

В более общем виде, пусть ${\displaystyle (X,{\mathcal {F}})}$ — произвольное измеримое пространство , а ${\displaystyle \mu }$ и ${\displaystyle \nu }$ — две меры на этом пространстве. Если найдется неотрицательная ${\displaystyle f}$ , позволяющая выразить меру ${\displaystyle \nu }$ через меру ${\displaystyle \mu }$ в виде

${\displaystyle \nu (A)=\int _{A}fd\mu ,}$

то такую функцию называют плотностью меры ${\displaystyle \nu }$ по мере ${\displaystyle \mu }$ , или производной Радона-Никодима меры ${\displaystyle \nu }$ относительно меры ${\displaystyle \mu }$ , и обозначают

${\displaystyle f={\frac {d\nu }{d\mu }}}$ .

Плотность случайной величины

Пусть определено произвольное вероятностное пространство ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$ , и ${\displaystyle X\colon \Omega \to \mathbb {R} ^{n}}$ случайная величина (или случайный вектор). ${\displaystyle X}$ индуцирует вероятностную меру ${\displaystyle \mathbb {P} ^{X}}$ на ${\displaystyle \left(\mathbb {R} ^{n},{\mathcal {B}}(\mathbb {R} ^{n})\right)}$ , называемую распределением случайной величины ${\displaystyle X}$ .

Если распределение ${\displaystyle \mathbb {P} ^{X}}$ абсолютно непрерывно относительно меры Лебега, то его плотность ${\displaystyle f_{X}={\frac {d\mathbb {P} ^{X}}{dx}}}$ называется плотностью случайной величины ${\displaystyle X}$ . Сама случайная величина ${\displaystyle X}$ называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

${\displaystyle \mathbb {P} (X\in B)=\int \limits _{B}f_{X}(x)\,dx}$ .

Замечания

• Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

• Функция распределения абсолютно непрерывной случайной величины ${\displaystyle X}$ непрерывна и может быть выражена через плотность следующим образом:

${\displaystyle F_{X}(x_{1},\ldots ,x_{n})=\mathbb {P} \left(X\in \prod \limits _{i=1}^{n}(-\infty ,x_{i}]\right)=\int \limits _{-\infty }^{x_{n}}\!\!\ldots \!\!\int \limits _{-\infty }^{x_{1}}f_{X}(x'_{1},\ldots ,x'_{n})\,dx'_{1}\ldots dx'_{n}}$ .

В одномерном случае:

${\displaystyle F_{X}(x)=\int \limits _{-\infty }^{x}f_{X}(x')\,dx'}$ .

Если ${\displaystyle f_{X}\in C(\mathbb {R} ^{n})}$ , то ${\displaystyle F_{X}\in {\mathcal {D}}(\mathbb {R} ^{n})}$ , и

${\displaystyle {\frac {\partial ^{n}}{\partial x_{1}\ldots \partial x_{n}}}F_{X}(x_{1},\ldots ,x_{n})=f_{X}(x_{1},\ldots ,x_{n})}$ .

В одномерном случае:

${\displaystyle {\frac {d}{dx}}F_{X}(x)=f_{X}(x)}$ .

• Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:

${\displaystyle \mathbb {E} [g(X)]=\int \limits _{\mathbb {R} ^{n}}g(x)\,\mathbb {P} ^{X}(dx)=\int \limits _{\mathbb {R} ^{n}}g(x)\,f_{X}(x)\,dx}$ ,

где ${\displaystyle g\colon \mathbb {R} ^{n}\to \mathbb {R} }$ — борелевская функция, так что ${\displaystyle \mathbb {E} [g(X)]}$ определено и конечно.

Плотность преобразования случайной величины

Пусть ${\displaystyle X\colon \Omega \to \mathbb {R} ^{n}}$ — абсолютно непрерывная случайная величина, и ${\displaystyle g\colon \mathbb {R} ^{n}\to \mathbb {R} ^{n}}$ — инъективная непрерывно дифференцируемая функция такая, что ${\displaystyle J_{g}(x)\not =0,\;\forall x\in \mathbb {R} ^{n}}$ , где ${\displaystyle J_{g}(x)}$ — якобиан функции ${\displaystyle g}$ в точке ${\displaystyle x}$ . Тогда случайная величина ${\displaystyle Y=g(X)}$ также абсолютно непрерывна, и её плотность имеет вид:

${\displaystyle f_{Y}(y)=f_{X}\left(g^{-1}(y)\right)\vert J_{g^{-1}}(y)\vert }$ .

В одномерном случае:

${\displaystyle f_{Y}(y)=f_{X}\left(g^{-1}(y)\right)\left\vert {\frac {dg^{-1}}{dy}}(y)\right\vert }$ .

Свойства плотности вероятности

• Плотность вероятности определена почти всюду . Если ${\displaystyle f}$ является плотностью вероятности ${\displaystyle \mathbb {P} }$ и ${\displaystyle f(x)=g(x)}$ почти всюду относительно меры Лебега, то и функция ${\displaystyle g}$ также является плотностью вероятности ${\displaystyle \mathbb {P} }$ ./

• Интеграл от плотности по всему пространству равен единице:

${\displaystyle \mathbb {P} \left(\mathbb {R} ^{n}\right)=\int \limits _{\mathbb {R} ^{n}}f(x)\,dx=1}$ .

Обратно, если ${\displaystyle f(x)}$ — неотрицательная почти всюду функция, такая что ${\displaystyle \int \limits _{\mathbb {R} ^{n}}f(x)\,dx=1}$ , то существует абсолютно непрерывная вероятностная мера ${\displaystyle \mathbb {P} }$ на ${\displaystyle \mathbb {R} ^{n}}$ такая, что ${\displaystyle f(x)}$ является её плотностью.

• Замена меры в интеграле Лебега:

${\displaystyle \int \limits _{\mathbb {R} ^{n}}\varphi (x)\,\mathbb {P} (dx)=\int \limits _{\mathbb {R} ^{n}}\varphi (x)\,f(x)\,dx}$ ,

где ${\displaystyle \varphi ::\mathbb {R} ^{n}\to \mathbb {R} }$ любая борелевская функция, интегрируемая относительно вероятностной меры ${\displaystyle {}\mathbb {P} }$ .

Примеры абсолютно непрерывных распределений

См. также

• Распределение вероятностей
• Сингулярное распределение
• Функция вероятности

Литература

• // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов . — М. : Большая российская энциклопедия, 2004—2017.