Interested Article - Последовательность

В математике последовательность — это пронумерованный набор каких-либо объектов, среди которых допускаются повторения, причём порядок объектов имеет значение. Нумерация чаще всего происходит натуральными числами . Более общие случаи см. в разделе .

В данной статье последовательность подразумевается бесконечной; случаи конечной последовательности оговариваются особо.

Примеры

Примеры числовой последовательности:

Примером конечной последовательности может служить последовательность домов на улице.
Многочлен от одной переменной $a_{0}+a_{1}x+\dots +a_{n}x^{n}$ $a_{0}+a_{1}x+\dots +a_{n}x^{n}$ можно рассматривать как конечную последовательность его коэффициентов, или бесконечную — в предположении $a_{i}=0$ $a_{i}=0$ при $i>n$ $i>n$ .
Последовательность простых чисел является одной из наиболее известных нетривиальных бесконечных числовых последовательностей .
Каждому действительному числу может быть сопоставлена собственная последовательность, называемая цепной дробью — причём для рациональных чисел она всегда конечна, для алгебраических иррациональных чисел бесконечна (для квадратичных иррациональностей — периодична ), а для трансцендентных чисел бесконечна и не периодична, хотя отдельные числа и могут встречаться в ней бесконечное число раз. Например, цепная дробь для числа ${\frac {13}{9}}$ ${\frac {13}{9}}$ конечна и равна $[1;2,4]$ $[1;2,4]$ , а цепная дробь числа π {\displaystyle \pi } уже бесконечна, не периодична и выглядит следующим образом: $[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1,84,2,1,1,15,\dots ]$ $[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1,84,2,1,1,15,\dots ]$ .
В геометрии часто рассматривается последовательность правильных многоугольников , форма которых зависит только от количества вершин.
Последовательность может состоять даже из множеств — к примеру, можно составить последовательность, в которой на $n$ $n$ -ой позиции находится множество всех многочленов степени $n$ $n$ с целыми коэффициентами от одной переменной.

Числовая последовательность

Строгое определение

Пусть задано некоторое множество $X$ $X$ элементов произвольной природы.

Всякое отображение $f\colon \mathbb {N} \to X$ $f\colon {\mathbb {N}}\to X$ множества натуральных чисел $\mathbb {N}$ $\mathbb {N}$ в заданное множество $X$ $X$ называется последовательностью (элементов множества $X$ $X$ ).

Обозначения

Последовательности вида

x_{1},x_{2},x_{3},\dots

x_{1},x_{2},x_{3},\dots

принято компактно записывать при помощи круглых скобок:

(x_{n})

(x_{n})

или

(x_{n})_{n=1}^{\infty }

(x_{n})_{{n=1}}^{{\infty }}

.

Иногда используются фигурные скобки:

\{x_{n}\}_{n=1}^{\infty }

\{x_{n}\}_{n=1}^{\infty }

.

Конечные последовательности могут записываться в следующем виде:

(x_{n})_{n=1}^{N}

(x_{n})_{{n=1}}^{N}

.

Также последовательность может быть записана как

(f(n))

(f(n))

,

если функция $f$ $f$ была определена ранее, или же её обозначение может быть заменено на саму функцию. Например, при $f(n)=n^{3}$ $f(n)=n^{3}$ последовательность можно записать в виде $(n^{3})$ $(n^{3})$ .

Связанные определения

Образ натурального числа $n$ $n$ , а именно элемент $x_{n}=f(n)$ $x_{n}=f(n)$ , называется $n$ $n$ - ым членом последовательности , а порядковый номер $n$ $n$ члена последовательности $x_{n}$ $x_{n}$ — его индексом .
Подмножество $f\left[\mathbb {N} \right]$ $f\left[{\mathbb {N}}\right]$ множества $X$ $X$ , которое образовано элементами последовательности, называется носителем последовательности : пока индекс пробегает множество натуральных чисел, точка, «изображающая» члены последовательности, «перемещается» по носителю.
Подпоследовательностью последовательности $(x_{n})$ $(x_{n})$ называется зависящая от $k$ $k$ последовательность $(x_{n_{k}})$ $(x_{{n_{k}}})$ , где $(n_{k})$ $(n_{k})$ — возрастающая последовательность натуральных чисел. Подпоследовательность можно получить из изначальной последовательности, выкинув из неё некоторые члены.

Замечания

Любое отображение множества $\mathbb {N}$ $\mathbb {N}$ в себя также является последовательностью.
Последовательность элементов множества $X$ $X$ может быть рассмотрена, как упорядоченное подмножество $X$ $X$ , изоморфное множеству натуральных чисел .

Способы задания числовых последовательностей

Жёлтая ромашковая головка, показывающая расположение в 21 (синяя) и 13 (аква) спиралей. Такие схемы, включающие **последовательности** чисел Фибоначчи, встречаются у самых разных растений

Аналитический , где формула определяет последовательность n-го члена, например: $a_{n}={\frac {n}{n+1}}$ $a_{n}={\frac {n}{n+1}}$
Рекуррентный , Например , числа Фибоначчи , где любой член последовательности выражается через предшествующие: $a_{1}=0,a_{2}=1,a_{n+2}=a_{n}+a_{n+1}$ $a_{1}=0,a_{2}=1,a_{n+2}=a_{n}+a_{n+1}$
Словесный ; Например , для любой бесконечной десятичной дроби можно построить последовательность её десятичных приближений по недостатку или избытку, округляя в каждой итерации дробь в меньшую или большую сторону.

Последовательность действий

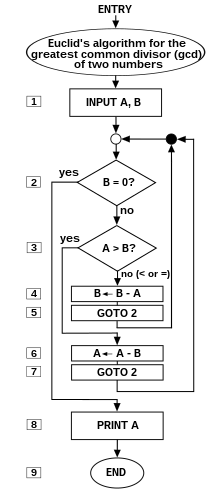
Блок-схема последовательности шагов (алгоритм Евклида) для вычисления наибольшего общего делителя (НОД) двух чисел a и b в точках с именами A и B. Алгоритм выполняется последовательным вычитанием в двух циклах: ЕСЛИ тест B ≥ A дает «да» или "истина" (точнее, число b в позиции B больше или равно числу a в позиции A) ТОГДА алгоритм определяет B ← B - A (что означает, что число b - a заменяет старое число b). Точно так же ЕСЛИ A> B, ТОГДА A ← A - B. Процесс завершается, когда (содержимое) B равно 0, что дает НОД в A. (Алгоритм, полученный из Scott 2009: 13; символы и стиль рисования из Tausworthe 1977).

«Алгоритм — это строгая и логичная последовательность действий для решения какой-либо задачи (математической, информационной и т. п.).»

Последовательности в математике

В математике рассматривают различные типы последовательностей:

числовые последовательности ;
последовательности элементов метрического пространства ;
временны́е ряды как числовой, так и не числовой природы;
последовательности элементов ;
последовательности состояний систем управления и автоматов .

Практически важные задачи, возникающие при изучении последовательностей:

Выяснение вопроса, конечна данная последовательность или бесконечна. Например, на 2020 год известно 51 простое число Мерсенна , но не доказано, что больше таких чисел нет.
Поиск закономерностей среди членов последовательности.
Поиск аналитической формулы, которая может служить хорошим приближением для $n$ $n$ -го члена последовательности. Например, для $n$ $n$ -го простого числа неплохое приближение даёт формула: $n\ln(n)$ $n\ln(n)$ (существуют и более точные).
Прогноз будущих состояний, в первую очередь выяснение вопроса, сходится ли данная последовательность к конечному или бесконечному пределу $($ $($ числовому или не числовому , в зависимости от типа множества $X).$ $X).$

Вариации и обобщения

Члены последовательности не обязательно должны нумероваться натуральными числами — к примеру, последовательность Фибоначчи может быть продолжена на отрицательные целые числа .
Существуют и так называемые многомерные последовательности , нумеруемые элементами декартова произведения $\mathbb {N} \times \mathbb {N} \times \dots \times \mathbb {N}$ $\mathbb {N} \times \mathbb {N} \times \dots \times \mathbb {N}$ . К таким относится, например, многомерное расширение последовательности Туэ-Морса . Также многочлен от нескольких переменных $x_{1},x_{2},\dots x_{n-1},x_{n}$ $x_{1},x_{2},\dots x_{n-1},x_{n}$ можно рассматривать как конечную $n$ $n$ -мерную последовательность, где на позиции $i_{1},i_{2},\dots i_{n-1},i_{n}$ $i_{1},i_{2},\dots i_{n-1},i_{n}$ находится коэффициент при произведении $x_{1}^{i_{1}}x_{2}^{i_{2}}\dots x_{n-1}^{i_{n-1}}x_{n}^{i_{n}}$ $x_{1}^{i_{1}}x_{2}^{i_{2}}\dots x_{n-1}^{i_{n-1}}x_{n}^{i_{n}}$ .

См. также

Примечания

Последовательность // . — М. : Советская Энциклопедия , 1984. — Т. 4. — С. 506—507. 21 января 2022 года.
Гусев В.А., Мордкович А.Г. Математика: справочные материалы (рус.) . — Москва: Просвещение, 1988. — 416 с.
Толковый словарь / под ред. Д. В. Дмитриева. — АСТ, Lingua, Астрель, 2003. — 1584 с. — ISBN 5-17-016483-1 , 5-271-05995-2.
И.Г.Семакин, А.П.Шестаков. . — Москва: Издательский центр "Академия", 2016. — С. 10. — 303 с. — ISBN 978-5-4468-3155-5 . 21 января 2022 года.