Конкретная математика
- 1 year ago
- 0
- 0


??????????? ( ??.-????. ?????????? < ?????? «????????; ?????») — ?????? ?????????? ????? , ????????????? ????????????? ?????????????? ????????? ? ???????????????? ????? . ? ????? ??????????? ?????????, ??? ????? ?? ?????????? ????? ????????? , ? ??????? ?????? ?? ????????, ????? ??????????? ?? ????????? ???????, — ?????? ???, ??????? ? ???????? ?????? ???????? ? ????????? ??? ??? ???? ?????????????? ?????? .
?????????? ??????????? ????????? ?? ?????? ???????? ????????, ????????? ? ???????? ????? ???????? . ?????????????? ??????? ????????? ????? ??????????? ??????? ???????? ??? ?????? ?????????????? ???????? ? ?????? ???? ??????? ?? ?????????? ????? .
?????????? ?? ????????? ? ???????????? ?????? , ?? ?????? ???????????? ? ??? ??? ??? ?????? ???????????? ?? ??????????, ??? ? ??? ????????? ????? ???????????. ??? ???????? ??????????????? ?????? , ??????????????? (?????) ???????? ???????? ?????? ??????; ??? ????? ??? ???????? ?? ??????????? ??????????? ? ???????????? ?????????? ????? ????? ??????? ??????? .
???????????????? ???????? ??????????? ???????? ???? ????????????? ? ???? ?????? , ???? ????????????? ? ??????????? ??????????????? ?????????????? ????????. ????? ?? ??????? ???????? ??????????? ?????? ?? ???? ??????? ????????? ?????? ???????? ???????? ( ??????? ). ??? ?????? ? ???????????? ???????? ?????????????? ?????? ???????????? ???????. ????? ???????, ????????????? ?????? ?? ???????????????? ? ?????????????? ???????????, ?????????? ???????? ????? ??????????? ???????????, ???????? ??????? ????? ???????? ????????? ??????????? ?????????? .
??????????? ?????????? ??????? ?? ?????????????, ??????????? ??????????? ?????? ???????????????????? ????????, ? ?????????? , ??????????????? ???? ?????? ?????? ?????? ? ?????????? ???????????, ?????? ????????? ?? ??? ???????? ??????????? ? ??????????? ?????????. ? ?????????, ?????????? ?????? ????? ??????????????? ? ??? ????? ??????????? ???? , ? ??? ????? ?????????????? ????; ???????? — ? ?????? , ? ??????????; ??????????? , ???????????? ?????????? ? ??????????? ????????? ??? ? ????????? , ??? ? ? ?????????????? ?????? ? ?. ?.
????? «??????????» ????????? ?? ??.-????. ?????? , ??? ???????? «????????, ??????, ?????», ? ??.-????. ??????????? , ????????????? ??????????? «?????????????, ??????????» , ??????? — «??????????? ? ????????», ???????????? ??????? «??????????? ? ??????????». ? ?????????, ?????????? ????? , ?? ?????? — ars mathematica , ???????? «????????? ??????????». ?????? ??.-????. ?????????? ? ??????????? ???????? ????? ????? «??????????» ??????????? ??? ? ?????? ?????????? (IV ??? ?? ?. ?.). ?? ?????? ??????? , ? ??????? ???? ????? ?????? ???? ????? ??????. matematyka , ???? ????? ???. mathematica .
? ??????? ?? ??????? ????? ????? «??????????», ??? ?????????? , ???????????, ?? ??????? ????, ? XVII ???? — ????????, ? ??????? ???????? ? «????? ????????? ??????? ? ?????? ????? ? ? ?????? ????????? ???????????» (1672 ???) .
?????????? ????????? ?????????? ??? «????? ? ??????????», ? ??? ??????????? ???????? ????????????? ?????? ?? XVIII ????.
???? ?? ?????? ??????????? ???????? ?????????? ??? ?????? :
? ??????? ?????????? ????????? ?????? ?? ?????, ? ??????? ??????????????? ???? ???????, ???? ????, ? ?????????? ?? ???????????, ????? ?? ??? ?????, ??????, ??????, ????? ??? ???-?????? ??????, ? ??? ???????????? ??? ????. ????? ???????, ?????? ???????????? ????? ????? ?????, ??????????? ??? ??????????? ? ??????? ? ????, ?? ????? ? ???????????? ??????? ??????? ?????????, ? ??? ????? ?????? ?????????? ?? ???????????, ?? ??????, ??? ???????? ? ???????????? ?????? ???????? ??????????.
???????????? ????? (???.) [ ???????? ?????? ]…illa omnia tantum, in quibus ordo vel mensura examinatur, ad Mathesim referri, nec interesse utrum in numeris, vel figuris, vel astris, vel sonis, aliove quovis obiecto talis mensura quaerenda sit; ac proinde generalem quamdam esse debere scientiam, quae id omne explicet, quod circa ordinem et mensuram nulli speciali materiae addicta quaeri potest, eamdemque, non ascititio vocabulo, sed iam inveterato atque usu recepto, Mathesim universalim nominari .
? ????????? ????? ???????????? ????????? ??????????? ?? ??? :464 , ?????? ?. ?. ???????????? :
??????????… ????? ? ?????????????? ?????????? ? ???????????????? ?????? ??????????????? ????.
??? ??????????? ?. ???????? ; ??????, ????? ?????????? ????????, ??? ??? ?????????????? ??????? ???? ???????? ? ????? ??????????? ? ??????????? ?????? :476,477 .
???????????? ??????? :
???????? ??????????… ?????????????? ?????? ??? ?????? ?? ?????????? ????? ?????????, ? ??????? ?????? ?? ????????, ????? ??????????? ?? ????????? ???????, — ?????? ???, ??????? ? ???????? ?????? ???????? ? ????????? ??????… ?????????? ???? ????? ??????????? ???? — ?????????????? ????????.
?????? ????? ??????????????? ?????? ??????????? ???? ???????????? ??????????? ???????? ??????????:
?????? ?? ?????????? ?????????? ? ? ???, ??? ???????????? ????? ? ???????? ????? ??????????, ???????? ????????. ?? ?? ????? ??????-?? ???????????, ??????? ????????, ? ????? ??????, ????? ????????????? ????? ?? ???? ??????, ? ????? ?? ?????? ???????, ??? ???????? «?????????????» ????? ????? ?????-?????? ??????? ? ??????? ????? ????????????.
«?????????????????» ????? ???????? ????? ?? ?????????? ?????????? ???????????? ????????, ??????? ????????????? ??? ????????????? ??????????, ????? ? ??????????, ?? ??????????????? ??? ???????????? ????? ?? ????????? ?????????????? ? ?? ????? ???? ??????????? .
1. ?????????? ??? ??????? ?????????? ?????????????? ? ?????????? ????????? ?? ???????????? ?????????? , ????????? ? ??????? ????? ? ???????????? ????????????:
? ?????? ?????????? , ????????? ?? ???????????????? ?????????????? ?????. ??????????, ???????? ? ?????? ?????? ??????????, ??????????? ? ??????????? ?? ?????????????.
????????? ???????? ?? ????????????? ?????????? ?????????? ?????????? ???????? ????????????:
2. ?????????? ??? ????????????? ??????? ?????????? ????????????? ??????????? ? ????? ?????????? ????????? ?????????????? ?? ?????????????:
3. ??? ?????????????? ??????? ????? ???????????? ?????? «??????????» ????????????? ?????????? ????????????? (???).
4. ???????????? ?????????????? ???????? () ?????????? ???? ???????? ??? ????????????? ???????? ??????????. ?? ?????????? . ???? ???????? ???????????? ???????????. ??????? ?????? — ??? . ?????????? ?????? — .
????????? ?????????? ???????? ? ??????????? ?????????????? ? ???????? ???????? ???????????, ??????? ??????????? ? ??? ????? ????? ??????. ??????????? ??????? ?????? ?????? ?????????????? ?? ?????? ??????????? ?????????????? ????????, ? ????? ???????????? ????????? ??????? ???????? ?????????? — ??????????????? ??????? , ?????????????? ?????? , ?????? ???????? ? ??. ????????? ??????? ???? ???????????? ????????? (?????????????? ??) ??????????????. ? ??????????? ?????????? ?????????????? ????? ??????? ??????????? ??????? ?????? (????????, ????????????? ????????? ), ??????? ????? ??????????? ??????????? ?? ?????? ?????? .

?????????? ?. ?. ???????????? ?????????? ????? ????????? ??????? ??????????:
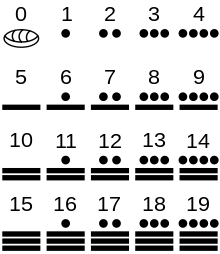
???????? ?????????? ???????? ?????? ? ???, ??? ??????? ???? ???????????? ?????????? ???????-?????? ???????? ??????. ??????? ?????????? — ????? ; ?????????? ????, ??? ??? ?????? ? ??? ?????????, ???????? ?? ??? ?? ????????, ????? ???-?? ?????, ? ?????? ???????? ??? ???? ?????? ????????, — ???????????? ?????????? ???????? ????????. ????? ????, ??? ??????? ???? ??????, ??? ??????? ?????????? ???????, ??? ????? ??????, ??? ????????? ? ??????????? ??????????, ?????, ??? ????? : ??? , ?????? , ???? . ?? ????????????? ????? ???????????? ??????? ?????? ??????????? ?????????? : ???????? , ????????? , ????????? ? ??????? ?????.
???????? ?????????? ????????? ?? ???????????? ? ?????? ?????????? ?????. ???????, ??????? ???? ??????? ???????? ?????????? ????? ????????? ???????? ?? ????? ??? ???????????? ?? ?? ?????????. ??????? ???? , ?? ???? ???? ??????? ????????????, ???????????? ? ????????? ???????? ??????, ????????? ??????? ??????? ?????????? ?????, ??? ?????????? ???? . ???????????? ????????? ????????? ?????? ????????? . ?????? ????????? ?????? ????? ???? ??????? ? ???????? ?????? , ????????? ?????????? ???????? ??????? . ??????? ??????????? ??????????? ??????????? ?????????? ??????? ????????? , ?????????? ????????? ???? .
??????????? ???????? ?????????????? ?????????? ????????? ??? ???????????? ????????????? ????? ??????? ? ???????????? ?????, ??? ????????? ?????? ? ??? ???????????? ??????????????? ??????? ?, ?????, ??? ??????? ????? ?????????? ?????. ?????? ?? ???? ???? ?????? ??????? ???? ? ??????? ???????? ??????????, ????????????? ? ???????? ???????? , ??????????? ? ?????????.
?????????? ??????? ????????????, ????????? ??????? ? ??????????? ????? ????, ????????? ?????????? ????. ? ????? ?????? ?????????????? ??????? ? ??????? ?? ??????????? ????? ???????????? ????-???? ? ?????????? ????. ??????? ?????? ??????????? ??????? ?????????? — ??????? ?????????????? ?????? , ?????????? ?????????? ???????????? ????????? ???????. ?????? ??????????-????????? — ?????????? ??????????? ????? ??????? ??????? ??? ?????????? ???? ????.
?????????? ?????????? ????? ?????????? ??? ??????? ?????????????? ??????? ? ???????????? ??? ?? ????????. ?????? ??????? ????????? ?? ??? ??? ?????, ? ?????? ????? ??????????? ??? ????? ???????? (????????????????). ????????, ?????? ?????????? ???????? ?????????, ?? ????? ???????????????? ?? ??? ????? ? ????? ? ??????????? ??? (????? ?? ???????? ?????) ?????. ???? ?? ??? ???? ??????, ??????? ?????????? ?????????, ???? ?? ?????? ?????? ??? ? ???, — ?? ????? ???????????????? ? ?? ?????, ??????? ? ?????? ?????? ???? ?????????????? — ??????????. ?????????? ? ???????????? ?????? ????? ????????? ? ????? ????? ???? — ???? ?? ??????? ??????????? ??????????????? ??????????.
?????? ???????????, ?????? ? ???????????????? — ????????? . ????????, ??????? ??????? « ???????????? » ?? ???????????? n-?????????. « ???????????? , ??? ???????? ?????????????? ????????. ???????, ?????? ?????????? ????????, ??????? ???????? ????????????? ??????????? ? ??????? ???????? » .
???????? ???????????????????? ????????, ??? ???????, ?????????? ??? ?????? ???????????????? ?????? : ??????? ??? ??????????? ???????? ????????????? ?????? ???????? ??????? ? ?????? , ? ????? ?? ?????? ? ??????? ?????? ?????? ???????? ?????????????? ??????? , ? ???????????? ?????????? ?????????????? ??????.
?????? ???????? ? ????????? ?????????? ?????????? ?? ?????? ??????? . ??????? ? XX ???? ??????????? ????????????? ???????? ? ???????, ??? ???????? ??????? ??????? ?????????????? ??????????????? , ?????? ??????????? ???????? ? ????????? ????, ??? ? ?????????? ??????? ?????????? ????????. ?????? ???????? ??????????? ??? ? ???????? ??????????? ? ??????????? ???????? ??????????, ??? ? ? ?????? ?????????? ?????? , ???????? ??????? ??? ??????????????? ????????????.
?????? ?????????????, ???????? ????????????????? ??????? ? ??????? ???????.
???????????? ????????????? ??? ?????????????? ??????? ? ?????? ?????? ????????, ???? ????? ? ???????????? ??????? — ???????? (???? ?????????? ????????? ??????, ???????????? ??). ?????? ?????? ????????? ? ???????? XX ???? ?????????????, ?????? ? ???????????????? ??????????? ?????????????? ????? ?? ?????? ????? ????????? ???? ??????????? ?????? ?? ???? ?????? ????????, ? ????????? ????????? ? ???????, ?????????????? ? ????????? ???????? ??????????. ????? ???????, ???? ? ?????? ???????? ????? ?????????? ????????????, ??? ?? ???????? ?? ????? ????????????? ??????????? ???????????.
?????? ?????? ???????????? ??????? ????????? ?????????????? ????????. ?????? ?????????, ?????????? ? ?????? ???????? ???? ????? ??????????? ??????, ??????????? ???????????? ? ????????.
?????? ?????? ???????????? ???????? ?????????? ?????? ?? ?????? ???????????? ?????? .
???????????? ???????????? ? ????????? ?????????? ???????????????? ?????? , ????? ???????????? ? ????????? ?????????????? (??, ??? ?????????, ? ????? ????????). ???????????? ????????? ?????????????? ?? ?????????? , ?????? ???????????????? ?????????????? ?????????? ????????????, ? ?????? ???????? ?????? ???????? — ?????????????? (????????????????).
?????????????? ?????????? — ??????? ? ????????????? ??????? ? ??????????, ????????? ?????????????? ?????????? [ ????????? ] . ???????? ???????? ???????????????? — « ???????????? — ?????? ???? ??????????? » . ???????? ???????????????? — ????? ??????? ??????????, ??? ???????? ?????????????????? .
???????? ??????, ??????????????? ?????????? ?????????? — ??????? . ??????? «?????» ????????????? ?????????? ?? ?????????????? ????????????? ? ?????????? ? ??????????? ?????? . ? ?????????? ???, ? ??????? ???????, ???? ?????????? ?????????????? ?? ????? , ???????????? , ?????????????? , ??????????? ? ?????? ?????.
|
|||||||||||||||
| ??????????? ????? | ??????????? | ||||||||||||||
????? — ??????????? ????? — ????? ????? — ???????????? ????? — ?????????????? ????? — ?????????????? ????? — ??????????????? ????? — ???????????? ????? — ??????????? ????? — ???????????????? ????? — ??????????? — ????????? — ????????? — ????????????? ????? — ??????????? ????? — p -????????? ????? — ?????????????? ?????????? — ???????? ????? — ????????????? —
??????? ?????????????? ? ????????? ? ????? ????? ???? ????????????? ?????? .
|

|
||
| ?????????? | ???????????????? ? ???????????? ?????????? | ????????? ?????? | ?????? |

|

|
||
| ???????????????? ????????? | ???????????? ??????? | ?????? ????? |
?????????? — ????????? ?????? — ?????? — ?????? ???? — ???????????????? ????????? — ???????????? ??????? — ?????? ?????
?????? ???????? — ???????? ??????? — ????? ??????? (????????, ? ?????????, ?????? ????? , ????????????? ??????? , ?????? ????????? ) — ?????????????? ????????? — ?????? ????? — ????????? .
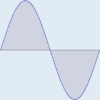
?????? ???????????????? ????????? ????????????? ????????? . ????????????? ????????????? ???????? ?????????????????? ??????? . ????????? ?????????????? ???????? ??????????? ??????????????? ??????? ?????????? ???????????????? ????????? . ???????? ???????????, ?????????? ??????????? ??? ??????????? ??????????? ? ???? ??????? ????????????? ??????? ????????? .
|
|

|

|

|

|
| ????????? | ????????????? | ???????????????? ????????? | ????????? | ???????? | ?????? ???? |
????????? — ????????????? — ?????????????? ????????? — ????????? — ???????????????? ????????? — ?????????????? ????????? — ???????? ??????? — ???????? — ?????? ???? .
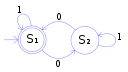
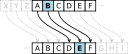
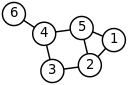
?????????? ?????????? ???????? ???????? ???????????? ????????, ????????? ????????? ?????? ????????? (??????????) ???????? (?? ???? ????????, ?? ????????? ?????????? ??????) .
|
|
|
|
| ?????????????? ?????? | ?????? ???????????? | ???????????? | ?????? ?????? |
????????????? — ?????? ???????? — ?????? ??????? — ?????????????? ?????? — ?????? ???????????? — ???????????? — ?????? ?????????????? ?????? — ?????? ?????? — ?????? ?????????? — ?????????? ?????????? — ??????????? .
????? ?????????? ???????? ?? ?????????? ? ??????? ??????????, ?????? ?????????? «??????????? ??????? ??? ???????????», ???????? ??????????? ?????? , ?????????? ? 1924 ???? ? ???????????? ?????? ?????? ???? ?????? ? ???????? ??????????????? ? ??????? 15 000 ????????? ???????? . ?? ????????? ???????? ?????????????? ????????? ??????????? ?????????? ????? ????????? ??????? ?????? ?? ?????????? ? ??????????:
????? ????, ? 2010 ???? ?? ????????? ???????? ????????? ????????? ?????? ???????? ?? ????????????? ??????????.
? 2000 ???? ?????????????? ???????? ???? ??????? ?????? ?? ???? ?????????????? ????? , ?? ??????? ?????? ?? ??????? ???????? ???? ? ??????? 1 ??? ???????? ??? .
?????????? ??????? ????? ??????, ??????????????? ?????? ??? ?????????????? ????????. ??????????? ?? ??? — ???????????? .
?????????????? ??????????? ??????????? ???????????: