Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары противоположных по направлению сил в его поперечной плоскости, точки приложения которых находятся на определённом удалении друг от друга. При этом данные силы образуют в поперечных сечениях тела единственный — крутящий момент . Примеры кручения: пружины растяжения-сжатия, валы.

При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения

${\displaystyle \varphi _{}={T\ell \over J_{0}G},}$

где:

${\displaystyle J_{0}}$ — геометрический полярный момент инерции ;

${\displaystyle \ell }$ — длина стержня;

G — модуль сдвига .

Отношение угла закручивания φ к длине ${\displaystyle \ell }$ называют относительным углом закручивания

${\displaystyle \theta ={\frac {\varphi }{\ell }}}$

Деформация кручения является частным случаем деформации сдвига .

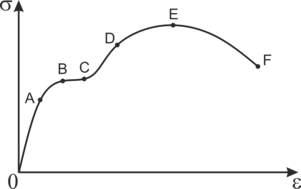
Напряжения при кручении

Вращающийся стержень, не работающий на кручение, называют валом . Стержень, используемый как упругий элемент, который работает на скручивание, называется торсионом . Касательные напряжения ${\displaystyle \tau _{r}}$ , возникающие в условиях кручения, определяются по формуле:

${\displaystyle \tau _{r}={T\cdot r \over J_{0}}}$ ,

где r — расстояние от оси кручения.

Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при ${\displaystyle r_{max}=R}$ и при максимальном крутящем моменте ${\displaystyle T_{max}}$ , то есть

${\displaystyle \tau _{max}={T_{max}\cdot R \over J_{0}}={\frac {T_{max}}{W_{p}}}}$ ,

где W _p — .

Это даёт возможность записать условие прочности при кручении в таком виде:

${\displaystyle \tau _{max}={\frac {T_{max}}{W_{p}}}\leq [\tau ]}$ .

Используя это условие, можно или по известным силовым факторам, которые создают крутящий момент Т, найти полярный момент сопротивления и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.

Это заготовка статьи по механике . Помогите Википедии, дополнив её.