Забывающий функтор ( стирающий функтор ) — теоретико-категорный функтор , который «забывает» некоторые или все алгебраические структуры и свойства исходной области, то есть переводит области, наделённые дополнительными структурами и свойствами, в кообласти с меньшими ограничениями.

Понятие не имеет строгого определения и используется для качественной характеризации преобразований, производимых такого рода функторами. Для алгебраической структуры с заданным набором операций эти преобразования можно описать как сокращение сигнатуры , например, забывающим является функтор, сопоставляющий каждому кольцу из категории колец ${\displaystyle \mathbf {Rng} }$ его аддитивную абелеву группу из категории ${\displaystyle \mathbf {Ab} }$ и переводящий гомоморфизмы колец в гомоморфизмы групп . Сигнатура может становится пустой, то есть кообластью такого функтора оказывается множество-носитель исходной структуры, примером такого функтора может служить преобразование групп из категории групп ${\displaystyle \mathbf {Grp} }$ во множества их элементов из категории ${\displaystyle \mathbf {Set} }$ , переводящее гомоморфизмы в «обычные» отображения множеств. Поскольку многие конструкции в математике описываются как множества с дополнительной структурой, забывающий функтор во множество-носитель является наиболее часто встречающимся примером на практике; возможность построения забывающего функтора в категорию множеств лежит в основе важного понятия конкретной категории . Кроме того, забывающий функтор может сохранять структуры, но при этом снижать ограничения по свойствам .

Пример

В качестве примера можно привести несколько забывающих функторов из категории коммутативных колец. Коммутативное кольцо, описанное на языке универсальной алгебры — это набор < R , +, *, a , 0, 1 > , удовлетворяющий определённым аксиомам; здесь + и * — бинарные операции на множестве R , a — унарная операция (взятие противоположного элемента по сложению), 0 и 1 — нульарные операции взятия тождественных элементов по сложению и умножению. Удаление единицы соответствует забывающему функтору в категорию колец без единицы; удаление * и 1 соответствует функтору в категорию абелевых групп , который сопоставляет каждому кольцу его группу по сложению. При этом каждому морфизму колец сопоставляется та же самая функция , только рассматриваемая как морфизм абелевых групп. Удаление всей сигнатуры соответствует функтору в категорию множеств.

Стирание структуры и свойств

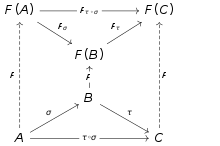
Есть определённые различия между теми функторами, которые «забывают структуру», и теми, которые «забывают только свойства». Если функторы ${\displaystyle \mathbf {Rng} \to \mathbf {Ab} }$ и ${\displaystyle \mathbf {Grp} \to \mathbf {Set} }$ «стирают» операции, то в качестве примера функтора, теряющего свойства, можно привести преобразование из категории абелевых групп в категорию групп , утрачивающий аксиому коммутативности умножения, но сохраняющий все операции.

Забывающие функторы почти всегда являются унивалентными . Например, конкретные категории определяются как категории, допускающие унивалентный функтор в категорию множеств. Функторы, забывающие аксиомы , всегда будут вполне унивалентными .

Левый сопряжённый функтор

Забывающие функторы довольно часто имеют левые сопряжённые функторы , которые конструируют ( англ. ). Например:

• свободный модуль : забывающий функтор из ${\displaystyle \mathbf {Mod} (R)}$ (категории ${\displaystyle R}$ - модулей ) в ${\displaystyle \mathbf {Set} }$ имеет левый сопряжённый ${\displaystyle \operatorname {Free} _{R}}$ , соответствующий отображению ${\displaystyle X\mapsto \operatorname {Free} _{R}(X)}$ , множества ${\displaystyle X}$ в свободный ${\displaystyle R}$ -модуль с базисом ${\displaystyle X}$ ;
• свободная группа ;
• тензорная алгебра .

В данном случае сопряжённость интерпретируется следующим образом: взяв множество X и построенный на нём объект (например, модуль M ), отображения множеств ${\displaystyle X\to M}$ однозначно соответствуют отображениям модулей ${\displaystyle \operatorname {Free} _{R}(X)\to M}$ . В случае векторных пространств об этом обычно говорят так: «отображение задаётся образами базисных векторов, и базисные вектора можно отправить куда угодно», этот факт выражается формулой:

${\displaystyle \operatorname {Hom} _{\mathbf {Mod} _{R}}(\operatorname {Free} _{R}(X),M)=\operatorname {Hom} _{\mathbf {Set} }(X,\operatorname {Forget} (M))}$ .

— пример категории, где забывающий функтор не имеет сопряжённого: не существует поля, удовлетворяющего свободному универсальному свойству для множества X .

Литература

• Маклейн, Саундерс . Категории для работающих математиков = Categories for the Working Mathematician. — М. : Физматлит, 2004. — С. 25. — 352 с. — ISBN 5-9921-0400-4 .