Interested Article - Модель биологического нейрона

- 2021-11-07
- 1
Моде́ль биологи́ческого нейро́на — математическое описание свойств нейронов , целью которого является точное моделирование процессов, протекающих в таких нервных клетках. В отличие от подобного точного моделирования, при создании сетей из искусственных нейронов обычно преследуются цели повышения эффективности вычислений.
Искусственные нейроны
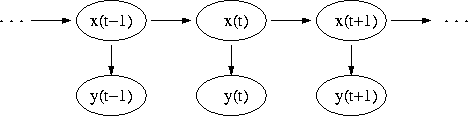
Простейшая модель сети из искусственных нейронов состоит из вектора нейронов, каждый из которых имеет вектор входных данных, вектор весов синапсов и, опционально, передаточную функцию , определяющую результат на выходе нейрона. Подобная модель может быть описана следующей формулой:
где y j — выход j -го нейрона, x i — i -й вход (входные данные) нейрона, w ij — синаптический вес на i -м входе j -го нейрона, а φ — активационная функция. Ранние попытки описать работу нейрона математической формулой принимали подобный вид, пока не были вытеснены кинетическими моделями — такими, как модель Ходжкина — Хаксли .
Биологическая абстракция
В случае моделирования поведения биологического нейрона, вместо вышеописанных абстракций (таких, как «вес синапса» и «передаточная функция»), используются модели физических процессов. Вход нейрона может быть описан как течение ионов, ток сквозь клеточную мембрану, возникающий при активации нейротрансмиттерами ионных каналов. В модели вход представлен функцией величины силы тока в зависимости от времени I ( t ) . Клетка ограничена изолирующей клеточной мембраной как диэлектриком , внутри и извне которой сконцентрированы заряженные ионы. Этот факт позволяет рассматривать мембрану как конденсатор и ввести значение ёмкости C m . Также нейрон реагирует на входной сигнал изменениями напряжения , или разности потенциалов между клеткой и окружением, наблюдаемыми как периодические скачки (спа́йки — от англ. spike ) и именуемыми « потенциал действия ». Величина напряжения представлена как V m и является искомым выходом нейрона.
Метод «интегрировать-и-сработать»
Одна из ранних моделей нейрона была предложена в 1907 Луи Лапиком ( фр. Louis Lapicque ) . Модель была описана следующей формулой:
которая есть производная по времени закона ёмкости , Q = CV . Когда на вход подаётся некий ток, разность потенциалов (напряжение) на мембране возрастает со временем, пока не достигает некоторого значения V th , при котором происходит скачкообразное изменение потенциала на выходе и напряжение сбрасывается до остаточного потенциала. После этого алгоритм повторяет работу с начала, пока опять не накопит энергии на следующее срабатывание. Такая схема имеет существенный недостаток — бесконечно большое линейное возрастание частоты срабатывания при линейном увеличении входного тока, что возможно только в абсолютно идеальных условиях без утечек.
Уточнить модель позволяет введение рефрактерного периода t ref , который ограничивает частоту срабатывания, запрещая срабатывание в течение некоторого времени после возникновения потенциала действия. Частота срабатывания в таком случае может быть описана как функция от постоянного тока следующей формулой:
- .
Недостаток этого подхода заключается в проявлении свойств независимой от времени памяти. Если модель получает некий заряд, недостаточный для срабатывания, она сохраняет его до следующего срабатывания. Если срабатывания не произойдёт — напряжение будет сохраняться вечно, что явно не соответствует процессам, наблюдаемым в реальной мембране.
Метод «интегрировать-и-сработать» с утечками
Дальнейшее усовершенствование вышеописанной модели решает указанный недостаток вечной памяти путём введения концепции утечки. Метод симулирует диффузию ионов, происходящую на поверхности мембраны в случае недостижения условий для генерации потенциала действия. Улучшенная подобным образом модель может быть описана следующей формулой:
где R m — значение электрического сопротивления мембраны. Теперь, чтобы сгенерировать потенциал действия, необходимо, чтобы значение тока на входе превысило некоторый порог I th = V th / R m . Иначе происходит утечка, аннулируя любые изменения потенциала. Частота срабатывания принимает следующий вид:
что сходится с предыдущей моделью (без утечки) для больших величин тока .
Модель Ходжкина — Хаксли
Эта модель, получившая широкое распространение, основана на кинетической модели Маркова. Модель разработана на основе совместного труда Алана Ходжкина и Эндрю Хаксли , датированного 1952 годом. Их труд основывался на данных, полученных в опытах с . Введённая ранее зависимость напряжения от тока доводится до зависимости напряжения от многих входных сигналов:
- .
Величина каждого входного сигнала может быть высчитана по закону Ома как
где g ( t , V ) — параметр проводимости , обратный сопротивлению, который возможно разложить на её постоянное среднее ḡ , а также на активационную m и инактивационную h составляющие. Это определит, сколько ионов может пройти сквозь доступные мембранные каналы. Среднее может быть вычислено по формуле:
а составляющие m и h подчиняются кинетикам первого порядка
с сходной динамикой для h , где возможно использовать τ и m ∞ , либо α и β в качестве определяющих порог параметров.
Подобная форма представления позволяет включить любые токи. Обычно включают «втекающие» Ca 2+ и Na + , а также несколько видов «вытекающих» K + , не забывая про ток «утечки». Конечный результат включает как минимум 20 различных параметров, которые необходимо определить и откалибровать для точного функционирования модели. Для сложных систем из большого количества нейронов вычислительная сложность, необходимая для работы модели, достаточно велика. Поэтому для практического применения зачастую требуются значительные упрощения.
Фицхью — Нагумо
В 1961—1962 годах Фицхью и Нагумо предложили упрощения, применимые к модели Ходжкина — Хаксли. Модель описывает «регенеративное самовозбуждение» посредством нелинейной положительной обратной связи напряжения на мембране, а также «восстановление» посредством линейной отрицательной обратной связи напряжения на затворе.
где, как и прежде, имеется мембранное напряжение и входной ток с slower general gate voltage w , а также параметры, найденные экспериментально a = −0.7, b = 0.8, τ = 1/0.08 . Несмотря на неочевидность соответствия модели биологическим исследованиям, она довольно хорошо описывает динамику, имея при этом небольшую сложность .
См. также
Примечания
- В разных источниках можно встретить и другие названия — такие, как «активационная функция», «логистическая функция», «трансфер-функция».
- Abbott, L.F. (англ.) // : journal. — 1999. — Vol. 50 , no. 5/6 . — P. 303—304 . — doi : . — . 13 июня 2007 года.
- Koch, Christof ; Idan Segev. Methods in Neuronal Modeling (англ.) . — 2. — Cambridge, MA: Massachusetts Institute of Technology , 1998. — ISBN 0-262-11231-0 .
- Izhikevich, Eugene M.; Richard FitzHugh .: . Scholarpedia . Дата обращения: 25 ноября 2007. 28 декабря 2012 года.
Внешние ссылки
- 2021-11-07
- 1




![f(I) =
\begin{cases}
0, & I \le I_\mathrm{th} \\
{[} t_\mathrm{ref}-R_\mathrm{m} C_\mathrm{m} \log(1-\tfrac{V_\mathrm{th}}{I R_\mathrm{m}}) {]}^{-1}, & I > I_\mathrm{th}
\end{cases}](/images/006/212/6212515/5.jpg?rand=801848)