Interested Article - Ортодиагональный четырёхугольник

- 2021-06-05
- 2

В евклидовой геометрии ортодиагональный четырёхугольник — это четырёхугольник , в котором диагонали пересекаются под прямым углом .
Специальные случаи
Дельтоид является ортодиагональным четырёхугольником, в котором одна диагональ является осью симметрии. Дельтоиды — это в точности ортодиагональные четырёхугольники, имеющие окружность , касающуюся всех четырёх сторон. Таким образом, дельтоиды являются описанными ортодиагональными четырёхугольниками .
Ромб — это ортодиагональный четырёхугольник с двумя парами параллельных сторон (т.е. ортодиагональный четырёхугольник и параллелограмм одновременно).
Квадрат — это частный случай ортодиагонального четырёхугольника, который является одновременно и дельтоидом, и ромбом.
Ортодиагональные равнодиагональные четырёхугольники, в которых диагонали не меньше любой стороны, имеют максимальный диаметр среди всех четырёхугольников, что решает случай n = 4 задачи наибольшего по площади многоугольника единичного диаметра . Квадрат является одним из таких четырёхугольников, но есть бесконечно много других.
Описание

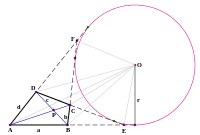
Антимедиатрисы выделены синим (основанием антимедиатрисы, опущенной из M xy является точка A xy ).
Середины сторон и основания антимедиатрис лежат на одной окружности. На рисунке точка O — центр этой окружности.
Для любого ортодиагонального четырёхугольника суммы квадратов противоположных сторон равны — для сторон a , b , c и d мы имеем :
Это следует из теоремы Пифагора , по которой любая из этих двух сумм равна сумме четырёх квадратов расстояний от вершин четырёхугольника до точки пересечения диагоналей.
Обратно — любой четырёхугольник, в котором a 2 + c 2 = b 2 + d 2 , должен быть ортодиагональным . Это можно показать разными путями, используя теорему косинусов , вектора , доказательство от противного и комплексные числа .
Диагонали выпуклого четырёхугольника перпендикулярны тогда и только тогда, когда бимедианы имеют одинаковую длину .
Диагонали выпуклого четырёхугольника ABCD перпендикулярны также тогда и только тогда, когда
- ,
где P — точка пересечения диагоналей. Из этого равенства следует почти немедленно, что диагонали выпуклого четырёхугольника перпендикулярны также тогда и только тогда, когда проекции пересечения диагоналей на стороны четырёхугольника являются вершинами вписанного четырёхугольника .

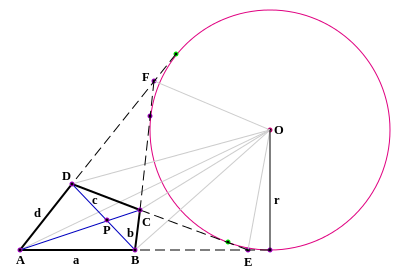
Прямоугольник, образованный точками пересечения нормалей с противоположными сторонами, выделен красным цветом (вершины прямоугольника — R, S, T, U.
Основания нормалей и пересечения нормалей с противолежащими сторонами лежат на одной окружности. На рисунке точка O — центр этой окружности.
Выпуклый четырёхугольник ортодиагонален тогда и только тогда, когда его параллелограмм Вариньона (вершинами которого служат середины сторон) является прямоугольником . Также выпуклый четырёхугольник ортодиагонален тогда и только тогда, когда середины его сторон и основания четырёх антимедиатрис являются восемью , окружности восьми точек . Центр этой окружности является центроидом четырёхугольника. Четырёхугольник, образованный основаниями антимедиатрис, называется главным орточетырёхугольником .
Если нормали к сторонам выпуклого четырёхугольника ABCD через пересечение диагоналей пересекают противоположные стороны в точках R , S , T , U , а K , L , M , N — основания нормалей, то четырёхугольник ABCD ортодиагонален тогда и только тогда, когда восемь точек K , L , M , N , R , S , T и U лежат на одной окружности, второй окружности восьми точек . Кроме того, выпуклый четырёхугольник ортодиагонален тогда и только тогда, когда четырёхугольник RSTU является прямоугольником, стороны которого параллельны диагоналям четырёхугольника ABCD .

Медианы выделены красным. Основания медиан являются центрами описанных окружностей.
Есть несколько соотношений относительно четырёх треугольников , образованных точкой пересечения диагоналей P и вершинами выпуклого четырёхугольника ABCD . Обозначим через m 1 , m 2 , m 3 , m 4 медианы в треугольниках ABP , BCP , CDP , DAP из P на стороны AB , BC , CD , DA соответственно. Обозначим через R 1 , R 2 , R 3 , R 4 радиусы описанных окружностей , а через h 1 , h 2 , h 3 , h 4 — высоты этих треугольников. Тогда четырёхугольник ABCD ортодиагонален тогда и только тогда, когда выполняется любое из следующих равенств :
Более того, четырёхугольник ABCD с точкой пересечения диагоналей P ортодиагонален тогда и только тогда, когда центры описанных вокруг треугольников ABP , BCP , CDP и DAP окружностей являются серединами сторон четырёхугольника .
Сравнение с описанным четырёхугольником
Некоторые числовые характеристики описанных четырёхугольников и ортодиагональных четырёхугольников очень похожи, что видно в следующей таблице . Здесь длины сторон четырёхугольника равны a , b , c , d , радиусы описанных окружностей вокруг треугольников равны R 1 , R 2 , R 3 , R 4 , а высоты равны h 1 , h 2 , h 3 , h 4 (как на рисунке).
| Описанный четырёхугольник | Ортодиагональный четырёхугольник |
|---|---|
Площадь
Площадь K ортодиагонального четырёхугольника равна половине произведения длин диагоналей p и q :
Обратно — любой выпуклый четырёхугольник, площадь которого равна половине произведения диагоналей, ортодиагонален . Ортодиагональный четырёхугольник имеет наибольшую площадь среди всех выпуклых четырёхугольников с данными диагоналями.
Другие свойства
- Только для ортодиагональных четырёхугольников площадь не определяется однозначно сторонами и углом между диагоналями . Например, если из двух ромбов со сторонами a (как у всех ромбов, у них диагонали перпендикулярны) один имеет меньший острый угол, то площади будут различными.
- Если на сторонах любого четырёхугольника (выпуклого, вогнутого или самопересекающегося) нарисовать квадраты , то их центры будут вершинами ортодиагонального четырёхугольника (к тому же и равнодиагонального ). Это утверждение носит название теоремы Ван-Обеля .
Свойства ортодиагонального вписанного четырёхугольника
Радиус описанной окружности и площадь
Пусть во вписанном в окружность ортодиагональном четырёхугольнике точка пересечения диагоналей делит одну из диагоналей на отрезки длиной p 1 и p 2 , а другую — на отрезки длиной q 1 и q 2 . Тогда (первое равенство в Утверждении 11 в книге Архимеда « Леммы »)
- ,
где D — диаметр описанной окружности . Это выполняется для любых двух перпендикулярных хорд окружности . Из этой формулы вытекает выражение для радиуса описанной окружности
или, в терминах сторон четырёхугольника,
Отсюда также следует, что
Тогда, согласно формуле Эйлера , радиус описанной окружности может быть выражен в терминах диагоналей p и q и расстоянию x между серединами диагоналей
Формула для площади K вписанного ортодиагонального четырёхугольника в терминах четырёх сторон получается непосредственно, если скомбинировать теорему Птолемея и формулу .
Другие свойства
- Во вписанном ортодиагональном четырёхугольнике антицентр совпадает с точкой пересечения диагоналей .
- Теорема Брахмагупты утверждает, что для любого вписанного ортодиагонального четырёхугольника перпендикуляр к стороне, проходящий через точку пересечения диагоналей, делит пополам противоположную сторону .
- Если ортодиагональный четырёхугольник является вписанным, расстояние от центра описанной окружности до любой стороны равно половине длины противоположной стороны .
- Во вписанном ортодиагональном четырёхугольнике расстояние между серединами диагоналей равно расстоянию между центром описанной окружности и точкой пересечения диагоналей .
- Ортодиагональный четырёхугольник, являющийся также равнодиагональным , является среднеквадратным четырёхугольником , поскольку его параллелограмм Вариньона является квадратом. Его площадь может быть выражена чисто в терминах сторон.
Прямоугольники вписанные в ортодиагональный четырехугольник
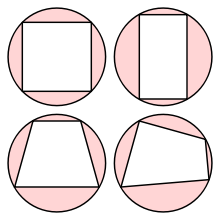
В любой ортодиагональный четырехугольник можно вписать бесконечно много прямоугольников, относящихся к следующим двум множествам:
- (i) прямоугольники, чьи стороны параллельны диагоналям ортодиагонального четырехугольника
- (ii) прямоугольники, определяемые окружностями точек Паскаля.


Примечания
- , p. 119—130.
- ↑ , p. 136—138.
- , p. 306—309.
- , p. 195–211.
- ↑ , p. 13–25.
- , p. 109–119.
- , p. 310–311.
- , p. 306–309.
- , p. 104–105, #4–23.
- David, Fraivert (2019), , , 23 : 5—27 от 23 октября 2020 на Wayback Machine .
- David, Fraivert (2017), (PDF) , , 17 : 509—526 от 5 декабря 2020 на Wayback Machine .
- Фрейверт, Д. М. (2019), , Математическое образование: современное состояние и перспективы : материалы Международной научной конференции от 10 ноября 2019 на Wayback Machine
Литература
- Martin Josefsson. Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral // Forum Geometricorum. — 2010. — Vol. 10. — P. 119–130.
- Martin Josefsson. Characterizations of Orthodiagonal Quadrilaterals // Forum Geometricorum. — 2012. — Vol. 12. — P. 13–25.
- Maria Flavia Mammana, Biagio Micale, Mario Pennisi. The Droz-Farny Circles of a Convex Quadrilateral // Forum Geometricorum. — 2011. — Vol. 11. — P. 109–119.
- N. Altshiller-Court. College Geometry. — Dover Publications, 2007. (Переиздание книги 1952 года, Barnes & Noble)
- Douglas W. Mitchell. // Mathematical Gazette. — 2009. — Vol. 93. — P. 306–309.
- Dan Ismailescu, Adam Vojdany. Class preserving dissections of convex quadrilaterals // Forum Geometricorum. — 2009. — Vol. 9. — P. 195–211.
- J. Harries. Area of a quadrilateral // Mathematical Gazette. — 2002. — No. 86.
- David Fraivert. // Forum Geometricorum. — 2017. — Vol. 17. — P. 509–526.
- Alfred S. Posamentier, Charles T. Salkind. . — New York: Dover Publ., 1996. — ISBN 0-486-69154-3 .
- 2021-06-05
- 2