Число Хееша фигуры — максимальное число слоёв копий той же фигуры, которые могут её окружать. Задача Хееша — это задача определения набора чисел, которые могут быть числами Хееша. И то, и другое названы именем немецкого геометра , который нашёл мозаику с числом Хееша 1 (объединение квадрата, правильного треугольника и треугольника с углами 30-60-90) и предложил более общую задачу .

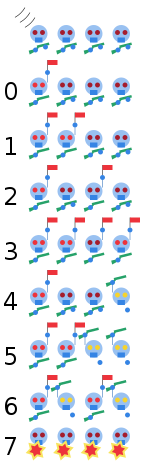
Например, квадрат может быть окружён бесконечным числом слоёв конгруэнтных квадратов в квадратном паркете , в то время как окружность нельзя окружить без дыр даже одним слоем равных окружностей. Число Хееша для квадрата бесконечно, а число Хееша окружности равно нулю. В более сложных примерах, таких, как на рисунке, многоугольная плитка может быть окружена несколькими слоями, но не бесконечным числом слоёв. Максимальное число слоёв является числом Хееша плитки.

Формальное определение

Замощение плоскости — это разрезание плоскости на области, называемые плитками . Нулевая корона плитки определяется как сама плитка, а для k > 0 k -ая корона — это множество плиток, имеющие общую точку с ( k − 1)-ой короной. Число Хееша фигуры S — это максимальное значение k , для которого существует замощение и плитка t в этом замощении, для которой все плитки от нулевой до k -ой короны плитки t конгруэнтны S . В некоторых работах дополнительно требуется, чтобы объединение корон от нулевой до k -ой было односвязной областью .

Если нет верхней границы числа слоёв, которыми плитка может быть окружена, говорят, что её число Хееша бесконечно. В этом случае, на основе леммы Кёнига можно показать, что существует замощение всей плоскости конгруэнтными копиями плитки .

Пример

Рассмотрим многоугольник P , показанный на рисунке справа, образованный из правильного шестиугольника путём добавления выступов на двух сторонах и выемок на трёх сторонах. Рисунок показывает замощение, состоящее из 61 копии P , одной бесконечной области и четырёх ромбов внутри четвёртого слоя. Первые четыре короны от центрального многоугольника состоят исключительно из копий плитки P , так что число Хееша равно по меньшей мере четырём. Невозможно распределить многоугольники так, чтобы избежать ромбовидных «дыр», поскольку 61 копия плитки P имеет слишком много впадин, чтобы выступы могли их заполнить. Таким образом, число Хееша плитки P равно в точности четырём. Согласно усиленному определению, чтобы корона была односвязной, число Хееша равно трём. Этот пример обнаружил .

Известные результаты

Неизвестно, всем ли положительным числам соответствуют числа Хееша. Первый пример многоугольника с числом Хееша 2 дала Анн Фонтен , показавшая, что бесконечное число фигур полимино обладают этим свойством . Кейзи Манн построил семейство плиток, каждая с числом Хееша 5, которое на настоящий момент является наибольшим известным. Плитки Манна имеют число Хееша 5 даже при строгих условиях, что каждая корона должна быть односвязной .

Для соответствующей задачи на гиперболической плоскости число Хееша может быть сколь угодно велико .

Примечания

Литература

• Тарасов А. С. О числе Хееша для плоскости Лобачевского // Математические заметки . — 2010. — Т. 88 , вып. 1 . — doi : .
• Dutch, Steven. The Heesch Tile: An Interesting Non-Tiler. — Natural and Applied Sciences, , 2008.
• Grünbaum B., Shephard G. C. . Heesch’s Problem // Tilings and Patterns. — W. H. Freeman, 1987. — P. 155–156.
• Fontaine, Anne. An infinite number of plane figures with Heesch number two // Journal of Combinatorial Theory. Ser. A. — 1991. — Vol. 57, no. 1. — doi : .
• Heesch H. . Regülares Parkettierungsproblem. — Cologne and Opladen: Westdeutscher Verlag, 1968. Как цитировано Грюнбаумом и Шепардом ( ) и Фонтани ( ).
• Mann, Casey. Heesch’s tiling problem // American Mathematical Monthly . — 2004. — Vol. 111, no. 6. — doi : .

Ссылки

• Eppstein, David. The Geometry Junkyard: Heesch’s Problem.
• Friedman, Erich. Heesch Tiles with Surround Numbers 3 and 4.
• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .