Interested Article - Цепная гомотопия

- 2021-02-17
- 1
Цепна́я гомото́пия — вариация понятия « гомотопия » в алгебраической топологии и гомологической алгебре
Определение
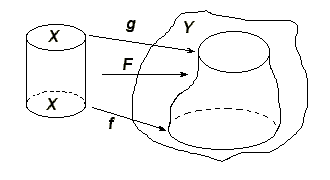
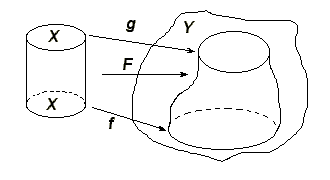
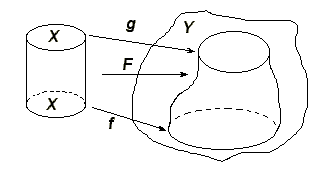
Пусть — цепной комплекс модулей (то есть семейство модулей и модульных гомоморфизмов ), и — цепные отображения комплекса в комплекс (то есть такие гомоморфизмы что ).
Цепной гомотопией между отображениями и называется такое семейство гомоморфизмов , что

Свойства
-
Если отображения
и
цепно гомотопны, то индуцированные отображения на
гомологиях
равны (где
). В самом деле, пусть
— цикл, то есть элемент из
. Тогда
. Так как
и
цепно гомотопны, то
- ,
- то есть отличаются на границу (элемент ).
- Для большинства теорий гомологий доказывается, что гомотопные непрерывные отображения топологических пространств индуцируют цепно гомотопные отображения комплексов и, по доказанному, одинаковые отображения групп гомологий (выполняется аксиома гомотопической инвариантности ).
Литература
- Вик Дж. У. Теория гомологий. Введение в алгебраическую топологию. — М. : МЦНМО, 2005
- Гельфанд С. И., Манин Ю. И. Методы гомологической алгебры. Введение в когомологии и производные категории. Том 1. — М. : Наука, 1989
- Дольд А. Лекции по алгебраической топологии. — М. : Мир, 1976
- Маклейн С. Гомология. — М. : Мир, 1966
- Спеньер Э. Алгебраическая топология. — М. : Мир, 1971
- 2021-02-17
- 1