Полный четырёхугольник (иногда употребляется термин полный четырёхвершинник ) — это система геометрических объектов, состоящая из любых четырёх точек на плоскости , никакие три из которых не лежат на одной прямой, и шести прямых, соединяющих шесть пар точек. Конфигурация, двойственная к полному четырёхугольнику — полный четырёхсторонник — является системой из четырёх прямых, никакие три из которых не проходят через одну точку, и шести точек пересечения этих прямых. Лахлан для полного четырёхугольника использовал название тетрастигма , а для полного четырёхстронника — тетрагам . Эти термины, хоть и редко, но встречаются в литературе.

Определения

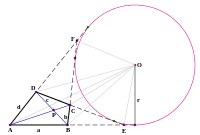
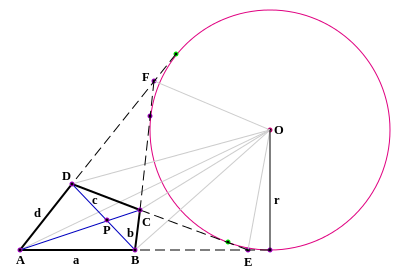
Фигура, состоящая из четырёх точек на плоскости, никакие три из которых не коллинеарны, и шести прямых, попарно их соединяющих, называется полным четырёхугольником . Стороны, не имеющие общей вершины в полном четырёхугольнике, называются противоположными . Точки пересечения трёх пар противоположных сторон называются диагональными точками .

Фигура, состоящая из четырёх прямых на плоскости, никакие три из которых не сходятся в одной точке, и шести точек попарного их пересечения, называется полным четырёхсторонником . Четыре прямые называются сторонами, а шесть точек — вершинами четырёхсторонника. Вершины, не примыкающие к одной и той же стороне, называются противоположными . Прямые, соединяющие три пары противоположных вершин, называются диагоналями .

Ряд из шести (пяти, четырёх) точек, в которых стороны полного четырёхугольника пресекают некоторую прямую, называется рядом точек, порождаемым полным четырёхугольником . Если такая прямая проходит через две диагональные точки A и C , а B и D — точки, в которых две остальные стороны пересекают прямую AC , то пары точек AC и BD называются гармонической четвёркой и обозначаются H(AC, BD) . Точки B и D называются гармоническими по отношению к A и C , а точка D (или B ) называется гармонически сопряжённой с точкой B (или D ) относительно пары точек A и D .

Если между точками двух фигур существует соответствие, такое, что прямые, соединяющие каждую пару соответственных точек, сходятся в некоторой точке O , то фигуры называются перспективными относительно центра O .

Если между прямыми линиями двух фигур существует соответствие, такое, что точки пересечения каждой пары соответственных прямых лежат на одной и той же прямой l , то эти фигуры называются перспективными относительно оси l .

После открытия плоскости Фано , конечной геометрии , в которой диагональные точки полного четырёхугольника коллинеарны , некоторые авторы добавляют к аксиомам проективной геометрии аксиому Фано , постулирующую, что диагональные точки не коллинеарны .

Проективные свойства

Как система точек и прямых, в которой все точки принадлежат одинаковому числу прямых, а все прямые содержат одинаковое число точек, полный четырёхугольник и полный четырёхсторонник являются проективными конфигурациями . В обозначениях проективных конфигураций полный четырёхугольник записывается как (4 ₃ 6 ₂ ), а полный четырёхсторонник — как (6 ₂ 4 ₃ ), где числа в этих обозначениях указывают число точек, число прямых, проходящих через каждую точку, число прямых и число точек на каждой прямой. Проективно двойственной конфигурацией полного четырёхугольника является полный четырёхсторонник, и наоборот. Для любых двух полных четырёхугольников или любых двух полных четырёхсторонников имеется единственное проективное преобразование , переводящее одну из конфигураций в другую .

Карл Штаудт преобразил основания математики в 1847 году, используя полный четырёхугольник, когда он заметил, что «свойства гармоничности» основываются на сопутствующих свойствах четырёхугольника — точки пересечения противоположных сторон четырёхугольника и пересечения диагоналей с прямой, проходящей через эти точки, образуют гармоническую четвёрку . Исследователи современной геометрии и алгебры обратили внимание на влияние Штаудта на Марио Пьери и Феликса Клейна .

Евклидовы свойства

Веллс описывает некоторые дополнительные свойства полных четырёхсторонников, в которых используются метрические свойства евклидовой плоскости , не являющиеся чисто проективными. Середины диагоналей коллинеарны и (как доказал Исаак Ньютон ) на той же прямой лежит центр конического сечения , касательного четырём прямым четырёхсторонника. Любые три прямые четырёхсторонника образуют стороны треугольника. Ортоцентры четырёх треугольников, образованных таким образом, лежат на другой прямой, перпендикулярной первой прямой (проходящей через середины диагоналей). Описанные окружности этих четырёх треугольников пересекаются в одной точке. Кроме того, три окружности, построенные на диагоналях как на диаметрах, принадлежат одному , ось которого проходит через ортоцентры.

Полярные круги треугольников полного четырёхсторонника образуют систему .

См. также

• Прямая Ньютона — Гаусса
• Коника девяти точек
• Четырёхугольник

Примечания

Литература

• Дж. В. Юнг. Проективная геометрия. — Москва: Государственное издательство ИНОСТРАННОЙ ЛИТЕРАТУРЫ, 1949.
• Roger A. Johnson. Advanced Euclidean Geometry. — Mineola, New York: Dover Publications, 2007. — ISBN 978-0-486-46237-0 . (Первоначальная публикация — 1960)
• H. S. M. Coxeter . Projective Geometry, 2nd ed.. — Springer-Verlag, 1987. — ISBN 0-387-96532-7 .
• Robin Hartshorne . Foundations of Projective Geometry. — W. A. Benjamin, 1967. — С. 53–6.
• Robert Lachlan. An Elementary Treatise on Modern Pure Geometry. — London, New York: Macmillan and Co., 1893. Ссылка из Исторических Математических Монографий Корнеллского университета
• David Wells. . — Penguin, 1991. — С. –36. — ISBN 0-14-011813-6 .

Ссылки

• Hazewinkel, Michiel, ed. (2001), , Encyclopedia of Mathematics , Springer , ISBN 978-1-55608-010-4
• (неопр.) . Cut-the-Knot . Дата обращения: 27 декабря 2016. 16 декабря 2016 года.
• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .