В теории категорий , представимый функтор — функтор специального типа из произвольной категории в категорию множеств . В некотором смысле, такие функторы задают представление категории в терминах множеств и функций.

Определение

Пусть C — локально малая категория , тогда для каждого её объекта A Hom( A ,-) — функтор Hom , который отправляет объекты X во множества Hom( A , X ).

Функтор F : C → Set называется представимым , если он естественно изоморфен Hom( A ,-) для некоторого объекта A категории C .

Контравариантный функтор G из C в Set , обычно называемый предпучком , представим, если он естественно изоморфен контравариантному hom-функтору Hom(-, A ) для некоторого объекта A категории C .

Универсальные элементы

Согласно лемме Йонеды , естественные преобразования Hom( A ,-) в F находятся во взаимно-однозначном соответствии с элементами F ( A ). Чтобы получить представление F , нам нужно узнать, для какого u ∈ F ( A ) соответствующее естественное преобразование — изоморфизм. Это мотивирует следующее определение:

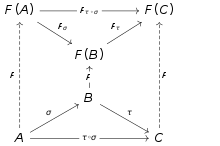
Универсальный элемент функтора F : C → Set — это пара ( A , u ), где A — объект C и u ∈ F ( A ), таких что для любой пары ( X , v ), v ∈ F ( X ) существует единственный морфизм f : A → X , такой что ( Ff ) u = v .

Естественное преобразование, индуцированное u ∈ F ( A ) является изоморфизмом тогда и только тогда, когда ( A , u ) — универсальный элемент. Поэтому на представления функтора часто ссылаются как на универсальные элементы. Из универсального свойства следует, что представление функтора единственно с точностью до единственного изоморфизма (впрочем, единственность следует и из полноты вложения Йонеды).

Примеры

• Рассмотрим контравариантный функтор P : Set → Set , который отправляет множество в его булеан , а функцию — во взятие полного прообраза подмножества. Для представления функтора нужна пара ( A , u ), такая что для любого множества X , множество Hom( X , A ) изоморфно P ( X ) через функцию Φ _X ( f ) = ( Pf ) u = f ⁻¹ ( u ). Возьмем A = {0,1}, u = {1}, соответствующая функция из X в A — характеристическая функция множества S .
• Забывающие функторы в Set очень часто представимы. В частности, забывающий функтор будет представим ( A , u ), если A — над синглентоном u .
  • Забывающий функтор Grp → Set из категории групп представим ( Z , 1).
  • Забывающий функтор Ring → Set из категории колец представим ( Z [ x ], x ).
  • Забывающий функтор Vect → Set из категории действительных векторных пространств представим ( R , 1).
  • Забывающий функтор Top → Set из категории топологических пространств представим топологическим пространством из одного элемента.

Связь с универсальными стрелками и сопряженными функторами

Категорные определения универсальной стрелки и сопряженных функторов могут быть выражены через представимые функторы.

Пусть G : D → C — функтор и X — объект C . Тогда ( A ,φ) — универсальная стрелка из X в G тогда и только тогда, когда ( A ,φ) — представление функтора Hom _C ( X , G -) из D в Set . Из этого следует, что G имеет левый сопряженный F тогда и только тогда, когда Hom _C ( X , G -) представим для всех X в C . Двойственные утверждения также верны.

Литература

• С. Маклейн Категории для работающего математика, — М. : ФИЗМАТЛИТ, 2004. — 352 с — ISBN 5-9221-0400-4 .