Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта , в которой все свободные тела движутся прямолинейно и равномерно либо покоятся . Существование систем, обладающих указанным свойством, постулируется первым законом Ньютона . Эквивалентное определение, удобное для использования в теоретической механике , звучит : «Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным , а время — однородным ». Экспериментальные факты свидетельствует о наличии систем с убедительной точностью близких к ИСО.

Второй и третий законы Ньютона, а также остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта . В соответствии с сильным принципом эквивалентности сил гравитации и инертности к инерциальным системам отсчёта также относятся надлежащим образом выбранные локально-инерциальные системы координат .

Термин «инерциальная система» ( нем. Inertialsystem ) был предложен в 1885 году Людвигом Ланге и означал систему координат, в которой справедливы законы Ньютона . По замыслу Ланге, этот термин должен был заменить понятие абсолютного пространства , подвергнутого в этот период уничтожающей критике. С появлением теории относительности понятие было обобщено до «инерциальной системы отсчёта».

Свойства инерциальных систем отсчёта

Всякая система отсчёта, движущаяся относительно ИСО равномерно, прямолинейно и без вращения, также является ИСО. Согласно принципу относительности , все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую . Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.

Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга равномерно, прямолинейно и поступательно со всевозможными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер , однородность пространства относительно сдвигов даст закон сохранения импульса , изотропность приведёт к сохранению момента импульса , а однородность времени — к сохранению энергии движущегося тела.

Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея .

В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости « c » (скорость распространения света в вакууме), и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца .

Связь с реальными системами отсчёта

Абсолютно инерциальные системы представляют собой математическую абстракцию и в природе не существуют. Однако существуют системы отсчёта, в которых относительное ускорение достаточно удалённых друг от друга тел (измеренное по эффекту Доплера ) не превышает 10 ⁻¹⁰ м/с², например, Международная небесная система координат в сочетании с Барицентрическим динамическим временем дают систему, относительные ускорения в которой не превышают 1,5⋅10 ⁻¹⁰ м/с² (на уровне 1σ) . Точность экспериментов по анализу времени прихода импульсов от пульсаров, а вскоре — и астрометрических измерений, такова, что в ближайшее время должно быть измерено ускорение Солнечной системы при её движении в гравитационном поле Галактики, которое оценивается в ${\displaystyle 2\cdot 10^{-10}}$ м/с² .

С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй , Солнцем , неподвижные относительно звёзд.

Геоцентрическая инерциальная система координат

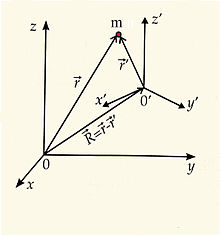
Применение Земли в качестве ИСО, несмотря на приближённый его характер, широко распространено в навигации . Инерциальная система координат, как часть ИСО строится по следующему алгоритму. В качестве точки O — начала координат выбирается центр земли в соответствии с принятой её моделью. Ось z совпадает с осью вращения земли. Оси x и y находятся в экваториальной плоскости. Следует заметить, что такая система не участвует во вращении Земли.

Примечания

См. также

• Увлечение инерциальных систем отсчёта
• Инвариантная производная по времени
• Неинерциальная система отсчёта